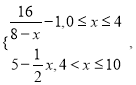题目内容
【题目】已知函数![]() ,
,![]() ,
,
⑴ 若![]() 有零点,求 m 的取值范围;
有零点,求 m 的取值范围;
⑵ 确定 m 的取值范围,使得![]() 有两个相异实根.
有两个相异实根.
【答案】(1) ![]() ;(2)
;(2) ![]() ;
;
【解析】
(1) ![]() 在x>0时有根,再对
在x>0时有根,再对![]() (2)记
(2)记![]() ,证明h(x)在(0,e)上单调递减,在(e,+∞)上单调递增,根据零点定理h(e)<0,解得
,证明h(x)在(0,e)上单调递减,在(e,+∞)上单调递增,根据零点定理h(e)<0,解得![]() ,再证明在(e,+∞)上只有一个零点,在(0,e)上只有一个零点,综上即可得解.
,再证明在(e,+∞)上只有一个零点,在(0,e)上只有一个零点,综上即可得解.
(1) ![]() 在x>0有根,当
在x>0有根,当![]() 时则
时则![]() 或m≤-2e(舍),当
或m≤-2e(舍),当![]() 时,f(0)=e2,则f(0)≤0无解,则m≥2e.
时,f(0)=e2,则f(0)≤0无解,则m≥2e.
(2)记![]() ,
,
则可以证明h(x)在(0,e)上单调递减,在(e,+∞)上单调递增,证明如下:
任取![]() ,令
,令![]() ,
, ![]() 由于
由于![]() ,
, ![]() ,
, ![]() 所以
所以![]() ,所以函数在(0,e)上单调递减;同理可证得在(e,+∞)上单调递增,
,所以函数在(0,e)上单调递减;同理可证得在(e,+∞)上单调递增,
所以h(e)为函数最小值,根据零点定理h(e)<0,解得![]() ,
,
以下说明必存在函数值大于零:
首先说明(e,+∞)上,当m≥2e时, ![]() ,当
,当![]() 时,
时, ![]() ;所以在(e,+∞)上只有一个零点。
;所以在(e,+∞)上只有一个零点。
再说明(0,e)上, ![]() ,所以取
,所以取![]() 即中
即中![]() 中较小值,当
中较小值,当![]() 即
即![]() 时,
时, ![]() ;当
;当![]() 即
即![]() 时,
时, ![]() ;所以在(0,e)上只有一个零点。
;所以在(0,e)上只有一个零点。
综上, ![]() .
.

练习册系列答案
相关题目