Question

【题目】已知F1 ， F2分别为椭圆C： + =1（a＞b＞0）的左、右两个焦点，椭圆上点M（ ， ）到F1、F2两点的距离之和等于4．
（1）求椭圆C的方程；
（2）已知过右焦点且垂直于x轴的直线与椭圆交于点N（点N在第一象限），E，F是椭圆C上的两个动点，如果kEN+KFN=0，证明直线EF的斜率为定值，并求出这个定值．

Answer 1

【答案】
（1）解：依据椭圆的定义2a=4a=2，

∵ 在椭圆 上，

∴ ，把a=2代入可得b2=3．

∴椭圆方程

（2）解：由（1）得，c=1，则N（1， ），

设直线NE的方程为： ，

代入 ，得 ．

设E（xE，yE），F（xF，yF），

∵点 在椭圆上，

∴由韦达定理得： ．

∴ ．

又直线NF的斜率与NE的斜率互为相反数，

在上式中以﹣k代k，可得 ，

∴xF+xE= ， ．．

∴直线EF的斜率

= ，

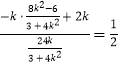即直线EF的斜率为定值，其值为

【解析】（1）由已知求得a，把已知的坐标代入椭圆方程得到关于a，b的关系式，把a代入求得b，则椭圆方程可求；（2）求出N的坐标，设出NE所在直线方程，与椭圆方程联立求得E的坐标，同理求得F的坐标，代入两点求斜率公式可得直线EF的斜率为定值．