题目内容
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨,生产每吨乙产品要用A原料1吨,B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是___________万元
【答案】获得最大利润为27万元.
【解析】试题分析:设生产甲产品![]() 吨,生产乙产品
吨,生产乙产品![]() 吨,则依题意可列出x,y的不等式组,然后画出不等式组表示的平面区域,利用目标函数的几何意义求出最值即可.
吨,则依题意可列出x,y的不等式组,然后画出不等式组表示的平面区域,利用目标函数的几何意义求出最值即可.
试题解析: 设生产甲产品![]() 吨,生产乙产品
吨,生产乙产品![]() 吨,则有关系:
吨,则有关系:
A原料 | B原料 | |
甲产品 | 3 | 2 |
乙产品 |
| 3 |
则有: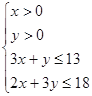 ,目标函数
,目标函数![]() ,不等式组表示的平面区域为四边形OABC(不包含线段OC、OA)及其内部, 如图所示,且B(3,4),而目标函数
,不等式组表示的平面区域为四边形OABC(不包含线段OC、OA)及其内部, 如图所示,且B(3,4),而目标函数![]() 可看作是直线
可看作是直线![]() 在y轴上的截距,显然在过点B时截距最大,且此时z最大,最大值为
在y轴上的截距,显然在过点B时截距最大,且此时z最大,最大值为![]() 万元.
万元.
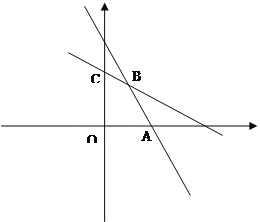
故当![]() =3,
=3,![]() =4时可获得最大利润为27万元,
=4时可获得最大利润为27万元,
答:生产甲产品3吨,乙产品4吨,可使该企业获得最大利润27万元.

【题目】甲乙两俱乐部举行乒乓球团体对抗赛.双方约定:
①比赛采取五场三胜制(先赢三场的队伍获得胜利.比赛结束)
②双方各派出三名队员.前三场每位队员各比赛﹣场
已知甲俱乐部派出队员A1、A2 . A3 , 其中A3只参加第三场比赛.另外两名队员A1、A2比赛场次未定:乙俱乐部派出队员B1、B2 . B3 , 其中B1参加第一场与第五场比赛.B2参加第二场与第四场比赛.B3只参加第三场比赛
根据以往的比赛情况.甲俱乐部三名队员对阵乙俱乐部三名队员获胜的概率如表:
A1 | A2 | A3 | |
B1 |
|
|
|
B2 |
|
|
|
B3 |
|
|
|
(1)若甲俱乐部计划以3:0取胜.则应如何安排A1、A2两名队员的出场顺序.使得取胜的概率最大?
(2)若A1参加第一场与第四场比赛,A2参加第二场与第五场比赛,各队员每场比赛的结果互不影响,设本次团体对抗赛比赛的场数为随机变量X,求X的分布列及数学期望E(X)


