题目内容
(本题满分18分,第1小题6分,第2小题6分,第3小题6分)
对于定义在D上的函数 ,若同时满足
,若同时满足
(Ⅰ)存在闭区间 ,使得任取
,使得任取 ,都有
,都有 是常数);
是常数);
(Ⅱ)对于D内任意 ,当
,当 时总有
时总有 ,则称
,则称 为“平底型”函数。
为“平底型”函数。
(1)判断 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;
(2)设 是(1)中的“平底型”函数,若
是(1)中的“平底型”函数,若 ,对一切
,对一切 恒成立,求实数
恒成立,求实数 的范围;
的范围;
(3)若 是“平底型”函数,求
是“平底型”函数,求 和
和 满足的条件,并说明理由。
满足的条件,并说明理由。
对于定义在D上的函数
 ,若同时满足
,若同时满足(Ⅰ)存在闭区间
 ,使得任取
,使得任取 ,都有
,都有 是常数);
是常数);(Ⅱ)对于D内任意
 ,当
,当 时总有
时总有 ,则称
,则称 为“平底型”函数。
为“平底型”函数。(1)判断
 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;(2)设
 是(1)中的“平底型”函数,若
是(1)中的“平底型”函数,若 ,对一切
,对一切 恒成立,求实数
恒成立,求实数 的范围;
的范围;(3)若
 是“平底型”函数,求
是“平底型”函数,求 和
和 满足的条件,并说明理由。
满足的条件,并说明理由。解:(1)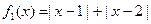 是“平底型”函数, ………………1分
是“平底型”函数, ………………1分
存在区间[1,2]使得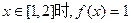 ,
,
当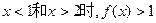 恒成立; ………………2分
恒成立; ………………2分
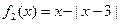 不是“平底型”函数, ………………1分
不是“平底型”函数, ………………1分
不存在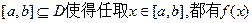 =常数 ………………1分
=常数 ………………1分
(2)若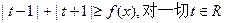 恒成立
恒成立
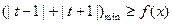
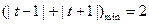 …………
………… ……3分
……3分
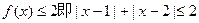
解得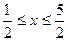 ………………3分
………………3分
(3)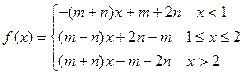
(1)当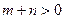 时
时
若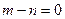 时,由图1b知,是“平底型”函数,存在[1,2]使
时,由图1b知,是“平底型”函数,存在[1,2]使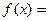 常数 …………1分
常数 …………1分
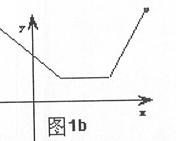
若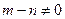 时,由图1a知,是“平底型”函数,存在[a,b]满足条件 …………1分
时,由图1a知,是“平底型”函数,存在[a,b]满足条件 …………1分
(2)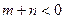 不是由图2知,不是“平底型”函数, …………1分
不是由图2知,不是“平底型”函数, …………1分
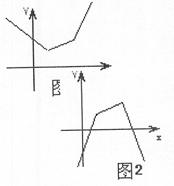
(3)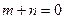 若
若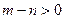 时,由图3知不是“平底型”函数,因为不存在区间[a,b]满足条件……1分
时,由图3知不是“平底型”函数,因为不存在区间[a,b]满足条件……1分
若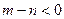 时,由图4
时,由图4 知不是“平底型”函数,因为不存在区间[a,b]满足条件 …………1分
知不是“平底型”函数,因为不存在区间[a,b]满足条件 …………1分
若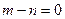 时,
时,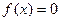 ,显然不是“平底型”函数 ………………1分
,显然不是“平底型”函数 ………………1分

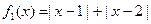 是“平底型”函数, ………………1分
是“平底型”函数, ………………1分存在区间[1,2]使得
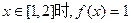 ,
,当
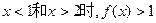 恒成立; ………………2分
恒成立; ………………2分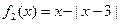 不是“平底型”函数, ………………1分
不是“平底型”函数, ………………1分不存在
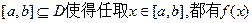 =常数 ………………1分
=常数 ………………1分(2)若
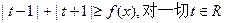 恒成立
恒成立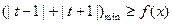
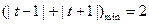 …………
………… ……3分
……3分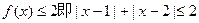
解得
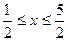 ………………3分
………………3分(3)
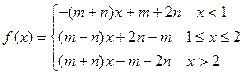
(1)当
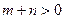 时
时若
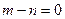 时,由图1b知,是“平底型”函数,存在[1,2]使
时,由图1b知,是“平底型”函数,存在[1,2]使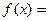 常数 …………1分
常数 …………1分
若
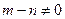 时,由图1a知,是“平底型”函数,存在[a,b]满足条件 …………1分
时,由图1a知,是“平底型”函数,存在[a,b]满足条件 …………1分(2)
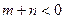 不是由图2知,不是“平底型”函数, …………1分
不是由图2知,不是“平底型”函数, …………1分
(3)
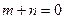 若
若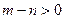 时,由图3知不是“平底型”函数,因为不存在区间[a,b]满足条件……1分
时,由图3知不是“平底型”函数,因为不存在区间[a,b]满足条件……1分若
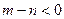 时,由图4
时,由图4 知不是“平底型”函数,因为不存在区间[a,b]满足条件 …………1分
知不是“平底型”函数,因为不存在区间[a,b]满足条件 …………1分若
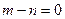 时,
时,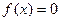 ,显然不是“平底型”函数 ………………1分
,显然不是“平底型”函数 ………………1分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
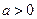 且
且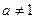 ,
,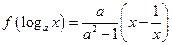
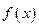 的表达式; (2)判断
的表达式; (2)判断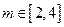 时,
时,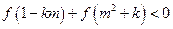 恒成立,求
恒成立,求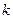 的取值范围.
的取值范围.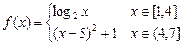 .
. 的大致图象;
的大致图象;
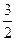 的零点.
的零点.
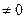 )恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1
)恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1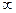 )上是增函数;
)上是增函数;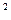 -5)<2.
-5)<2.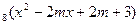 的定义域为R,则实数m的取值范围是
的定义域为R,则实数m的取值范围是 则f(ln3)=
则f(ln3)=
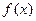 是
是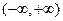 上的偶函数,若对于任意
上的偶函数,若对于任意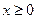 ,都有
,都有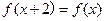 ,且当
,且当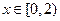 时,
时,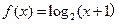 ,则
,则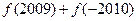 的值为( )
的值为( )



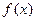 的定义域为实数集
的定义域为实数集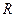 ,且满足
,且满足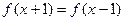 ,当
,当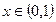 时,
时,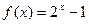 .则
.则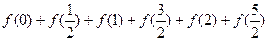 的值为 ( )
的值为 ( ) .
.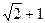 B.
B.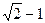 C.0 D.1-
C.0 D.1-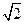
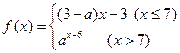
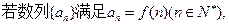 且
且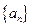 是递增数列,那么实数a的取值范围是 ( )
是递增数列,那么实数a的取值范围是 ( )


 .
.