题目内容

6．对任意实数x，x2-4bx+3b＞0恒成立，则b的取值范围是0＜b＜$\frac{3}{4}$．

分析 由题意可知△=16b2-12b＜0，进而求出b的范围．

解答 解：对任意实数x，x2-4bx+3b＞0恒成立，
∴△=16b2-12b＜0，
∴b（4b-3）＜0，
∴0＜b＜$\frac{3}{4}$．
故答案为0＜b＜$\frac{3}{4}$．

点评 考查了二次函数和二次不等式的关系．属于基础题型，应熟练掌握．

练习册系列答案
相关题目
16．已知数列{an}为等比数列，其前n项和为Sn，且S1，S2的等差中项为S3，若8（a1+a3）=-5．
（1）求数列[an]的通项公式；
（2）记Rn=|$\frac{1}{a_1}|+|\frac{2}{a_2}|+|\frac{3}{a_3}|+…+|\frac{n}{a_n}$|，对于任意的n≥2，n∈N*，不等式m（Rn-n-1）≥（n-1）2恒成立，求实数m的取值范围．
17．设a，b∈R，集合{a，1}={0，a+b}，则a-b=-1．
14．某商场2014年一月份到十二月份销售额呈现先下降后上升的趋势，下列函数模型中能较准确反映该商场月销售额f（x）与月份x关系的是（　　）
A．f（x）=a•bn（b＞0，且b≠1）B．f（x）=lognx+b（a＞0，且a≠1）
C．f（x）=x2+ax+bD．f（x）=$\frac{a}{x}+b$
1．函数y=$\frac{\sqrt{9-{3}^{x}}}{lg（x+1）}$的定义域为{x|-1＜x≤2，且x≠0}．
11．若函数f（x）=x2+bln（x+1）在其定义域内既有极大值又有极小值，则实数b的取值范围为（0，$\frac{1}{2}$）．
18．一船向正北航行，到达B处时，看见正西方向有相距10海里的两个灯塔C、D恰好与它在一条直线上，继续航行1小时后到达A处，看见一灯塔在船的南偏西60°方向，另一灯塔在船的南偏西75°方向（如图所示），则这只船的速度是5海里/小时．
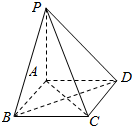15．如图，四棱锥P-ABCD中，PA⊥平面ABCD，ABCD为正方形，则该四棱锥中互相垂直的平面有6组．
16．求下列函数的最值：
（1）f（x）=x3-3x2+6x-2（-1≤x≤1）；
（2）f（x）=x+$\sqrt{1-{x}^{2}}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网