题目内容
11.若函数f(x)=x2+bln(x+1)在其定义域内既有极大值又有极小值,则实数b的取值范围为(0,$\frac{1}{2}$).分析 由题意先确定函数的定义域,再求导f′(x)=2x+$\frac{b}{x+1}$=$\frac{2{x}^{2}+2x+b}{x+1}$,从而可得b=-(2x2+2x)在(-1,+∞)上有两个不同的解,作函数的图象解得.
解答 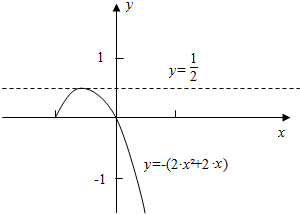 解:函数f(x)=x2+bln(x+1)的定义域为(-1,+∞),
解:函数f(x)=x2+bln(x+1)的定义域为(-1,+∞),
f′(x)=2x+$\frac{b}{x+1}$=$\frac{2{x}^{2}+2x+b}{x+1}$,
∵函数f(x)=x2+bln(x+1)在其定义域内既有极大值又有极小值,
∴f′(x)=2x+$\frac{b}{x+1}$=$\frac{2{x}^{2}+2x+b}{x+1}$=0在(-1,+∞)上有两个不同的解,
即2x2+2x+b=0在(-1,+∞)上有两个不同的解,
即b=-(2x2+2x)在(-1,+∞)上有两个不同的解,
作函数g(x)=-(2x2+2x)在(-1,+∞)上的图象如下,
,
结合图象可知,0<b<$\frac{1}{2}$;
故答案为:(0,$\frac{1}{2}$).
点评 本题考查了导数的综合应用及数形结合的思想应用,方程的解可化为函数的图象的交点问题,从而解得.

练习册系列答案
相关题目
2.若函数f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且f(2)=0,则使xf(x)<0的x的取值范围是( )
| A. | (-∞,-2) | B. | (-2,2) | C. | (2,+∞) | D. | (0,2)∪(-∞,-2) |
19.定义在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{3}}(x+1),x∈[0,2)}\\{-\frac{1}{2}{x}^{2}+4x-7,x∈[2,+∞)}\end{array}\right.$,则关于x的方程f(x)=a(0<a<1)的所有根之和为( )
| A. | 3-a-1 | B. | 1-3-a | C. | 3a-1 | D. | 1-3a |
16.不等式3x2+5x-2<0的解集为( )
| A. | (-∞,-2)∪($\frac{1}{3}$,+∞) | B. | (-2,$\frac{1}{3}$) | C. | [-2,$\frac{1}{3}$) | D. | (-2,$\frac{1}{3}$] |