题目内容
【题目】某市一所医院在某时间段为发烧超过38![]() 的病人特设发热门诊,该门诊记录了连续5天昼夜温差
的病人特设发热门诊,该门诊记录了连续5天昼夜温差![]() (
(![]() )与就诊人数
)与就诊人数![]() 的资料:
的资料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
昼夜温差 | 8 | 10 | 13 | 12 | 7 |
就诊人数 | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并说明昼夜温差(
,并说明昼夜温差(![]() )与就诊人数
)与就诊人数![]() 具有很强的线性相关关系.
具有很强的线性相关关系.
(2)求就诊人数![]() (人)关于出昼夜温差
(人)关于出昼夜温差![]() (
(![]() )的线性回归方程,预测昼夜温差为9
)的线性回归方程,预测昼夜温差为9![]() 时的就诊人数.
时的就诊人数.
附:样本![]()
![]() 的相关系数为
的相关系数为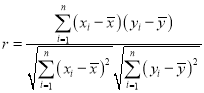 ,当
,当![]() 时认为两个变量有很强的线性相关关系.
时认为两个变量有很强的线性相关关系.
回归直线方程为![]() ,其中
,其中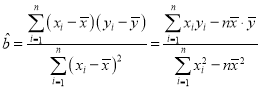 ,
,![]() .
.
参考数据:![]() ,
,![]()
【答案】(1)![]() ,有很强的线性相关关系;(2)可以预测昼夜温差为
,有很强的线性相关关系;(2)可以预测昼夜温差为![]() 时的就诊人数大约为21人左右.
时的就诊人数大约为21人左右.
【解析】
(1)根据已知数据,先求出![]() ,然后根据相关系数公式求出
,然后根据相关系数公式求出![]() 与
与![]() 比较,即可得出结果;
比较,即可得出结果;
(2)根据公式分别求出![]() ,
,![]() ,即可求出诊人数
,即可求出诊人数![]() (人)关于出昼夜温差
(人)关于出昼夜温差![]() (
(![]() )的线性回归方程,再将
)的线性回归方程,再将![]() 代入,可求出
代入,可求出![]() ,从而可预测昼夜温差为9
,从而可预测昼夜温差为9![]() 时的就诊人数.
时的就诊人数.
(1)![]() ,
,![]() ,
,
![]() ,
,
![]() ,昼夜温差
,昼夜温差![]() (
(![]() )与就诊人数
)与就诊人数![]() 具有很强的线性相关关系.
具有很强的线性相关关系.
(2)因为![]() ,
,
![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,
,
由此可以预测昼夜温差为![]() 时的就诊人数大约为21人左右.
时的就诊人数大约为21人左右.

 阅读快车系列答案
阅读快车系列答案【题目】某种设备随着使用年限的增加,每年的维护费相应增加现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如下表:
年份 | 1 | 2 | 3 | 4 | 5 |
维护费 | 1.1 | 1.6 | 2 | 2.5 | 2.8 |
(1)在这5年中随机抽取两年,求平均每台设备每年的维护费用至少有1年多于2万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程.若该设备的价格是每台16万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?请说明理由.
的线性回归方程.若该设备的价格是每台16万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?请说明理由.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式 .
.
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)现有![]() 人前去该商场购物,求获得纪念品的数量
人前去该商场购物,求获得纪念品的数量![]() 的分布列与数学期望.
的分布列与数学期望.