题目内容
【题目】一袋中有大小、形状相同的2个白球和10个黑球,从中任取一球.如果取出白球,则把它放回袋中;如果取出黑球,则该球不再放回,另补一个白球放到袋中.在重复![]() 次这样的操作后,记袋中的白球个数为
次这样的操作后,记袋中的白球个数为![]() .
.
(1)求![]() ;
;
(2)设![]() ,求
,求![]() ;
;
(3)证明:![]() .
.
【答案】(1)![]() (2)
(2) (3)证明见解析
(3)证明见解析
【解析】
(1)根据![]() 的取值以及概率,即可容易求得数学期望;
的取值以及概率,即可容易求得数学期望;
(2)求得当![]() 时,以及
时,以及![]() 时的概率,则问题得解;
时的概率,则问题得解;
(3)对第![]() 次白球个数的数学期望分为第
次白球个数的数学期望分为第![]() 次取出来的是白球,或者黑球进行讨论,即可证明.
次取出来的是白球,或者黑球进行讨论,即可证明.
(1)∵![]() 或
或![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
(2)∵当![]() 时,
时,![]() ,
,
当![]() 时,第
时,第![]() 次取出来有
次取出来有![]() 个白球的可能性有两种:
个白球的可能性有两种:
第![]() 次袋中有
次袋中有![]() 个白球,显然每次取出球后,球的总数保持不变,
个白球,显然每次取出球后,球的总数保持不变,
即袋中有![]() 个白球,
个白球,![]() 个黑球,第
个黑球,第![]() 次取出来的也是白球的概率为
次取出来的也是白球的概率为![]() ;
;
第![]() 次袋中有
次袋中有![]() 个白球,第
个白球,第![]() 次取出来的是黑球,由于每次总数为12个,
次取出来的是黑球,由于每次总数为12个,
故此时黑球数为![]() 个,这种情况发生的概率为
个,这种情况发生的概率为![]() ;
;
∴![]() ,
,
∴综上可知,
(3)∵第![]() 次白球个数的数学期望分为两类情况:
次白球个数的数学期望分为两类情况:
第![]() 次白球个数的数学期望为
次白球个数的数学期望为![]() ,由于白球和黑球的总数为12,
,由于白球和黑球的总数为12,
第![]() 次取出来的是白球的概率为
次取出来的是白球的概率为![]() ,
,
第![]() 次取出来的是黑球的概率为
次取出来的是黑球的概率为![]() ,此时白球的个数为
,此时白球的个数为![]() ,
,
∴![]()

即![]() .
.

【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,某学校140名老师均在微信好友群中参与了“微信运动”,对运动10000步或以上的老师授予“运动达人”称号,低于10000步称为“参与者”,为了解老师们运动情况,选取了老师们在4月28日的运动数据进行分析,统计结果如下:
推出的多款健康运动软件中的一款,某学校140名老师均在微信好友群中参与了“微信运动”,对运动10000步或以上的老师授予“运动达人”称号,低于10000步称为“参与者”,为了解老师们运动情况,选取了老师们在4月28日的运动数据进行分析,统计结果如下:
运动达人 | 参与者 | 合计 | |
男教师 | 60 | 20 | 80 |
女教师 | 40 | 20 | 60 |
合计 | 100 | 40 | 140 |
(Ⅰ)根据上表说明,能否在犯错误概率不超过0.05的前提下认为获得“运动达人”称号与性别有关?
(Ⅱ)从具有“运动达人”称号的教师中,采用按性别分层抽样的方法选取10人参加全国第四届“万步有约”全国健走激励大赛某赛区的活动,若从选取的10人中随机抽取3人作为代表参加开幕式,设抽取的3人中女教师人数为![]() ,写出
,写出![]() 的分布列并求出数学期望
的分布列并求出数学期望![]() .
.
参考公式: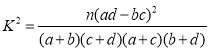 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】已知椭圆![]() 的一个顶点和两个焦点构成的三角形的面积为4.
的一个顶点和两个焦点构成的三角形的面积为4.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,试问,是否存在
两点,试问,是否存在![]() 轴上的点
轴上的点![]() ,使得对任意的
,使得对任意的![]() ,
,![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
【题目】某市一所医院在某时间段为发烧超过38![]() 的病人特设发热门诊,该门诊记录了连续5天昼夜温差
的病人特设发热门诊,该门诊记录了连续5天昼夜温差![]() (
(![]() )与就诊人数
)与就诊人数![]() 的资料:
的资料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
昼夜温差 | 8 | 10 | 13 | 12 | 7 |
就诊人数 | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并说明昼夜温差(
,并说明昼夜温差(![]() )与就诊人数
)与就诊人数![]() 具有很强的线性相关关系.
具有很强的线性相关关系.
(2)求就诊人数![]() (人)关于出昼夜温差
(人)关于出昼夜温差![]() (
(![]() )的线性回归方程,预测昼夜温差为9
)的线性回归方程,预测昼夜温差为9![]() 时的就诊人数.
时的就诊人数.
附:样本![]()
![]() 的相关系数为
的相关系数为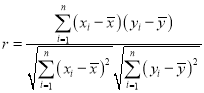 ,当
,当![]() 时认为两个变量有很强的线性相关关系.
时认为两个变量有很强的线性相关关系.
回归直线方程为![]() ,其中
,其中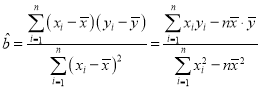 ,
,![]() .
.
参考数据:![]() ,
,![]()