Question

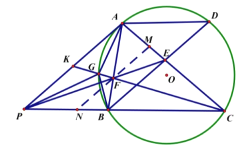
【题目】如图，AB、PA、PBC分别为⊙O的切线和割线，切点A是BD的中点，AC、BD相交于点E，AB、PE相交于点F，直线CF交⊙O于另一点G、交PA于点K.

证明：（1）K是PA的中点；（2）..

Answer 1

【答案】（1）见解析（2）见解析

【解析】

（1)在△APC中，由塞瓦定理，知.……①

∵A是BD的中点，PA是⊙O的切线，

∴∠PAB=∠ADB=∠ABD.

∴EB∥AP，. ………………………………………②

由①、②，得AK=KP.K是PA的中点.

另解：∴A是BD的中点，PA是⊙O的切线，

∴∠PAB=∠ADB=∠ABD，EB∥AP.

如图，过点F作MN∥AP，交AE于点M，交PB于点N.则

，.…………①

且EB∥AP∥MN，.…………②

∴由①、②，得.

∴FM=FN.

又由MN∥AP，得，

∴AK=KP，K是PA的中点.

（2）由（1）及切线长定理，得.因此，.

又∠PKG=∠CKP，

∴△PKG∽△CKP.

∠APG=∠KPG=∠KCP=∠GCB=∠BAG.

又∠PAG=∠ABG，

∴△GPA∽△GAB，.

.