题目内容
给出下列命题:①椭圆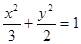 的离心率
的离心率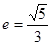 ,长轴长为
,长轴长为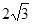 ;②抛物线
;②抛物线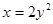 的准线方程为
的准线方程为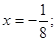 ③双曲线
③双曲线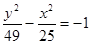 的渐近线方程为
的渐近线方程为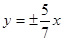 ;④方程
;④方程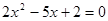 的两根可分别作为椭圆和双曲线的离心率.
的两根可分别作为椭圆和双曲线的离心率.
其中所有正确命题的序号是
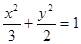 的离心率
的离心率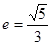 ,长轴长为
,长轴长为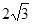 ;②抛物线
;②抛物线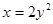 的准线方程为
的准线方程为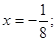 ③双曲线
③双曲线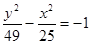 的渐近线方程为
的渐近线方程为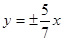 ;④方程
;④方程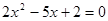 的两根可分别作为椭圆和双曲线的离心率.
的两根可分别作为椭圆和双曲线的离心率.其中所有正确命题的序号是
②④
略

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
题目内容
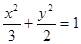 的离心率
的离心率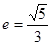 ,长轴长为
,长轴长为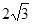 ;②抛物线
;②抛物线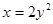 的准线方程为
的准线方程为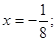 ③双曲线
③双曲线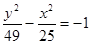 的渐近线方程为
的渐近线方程为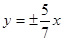 ;④方程
;④方程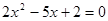 的两根可分别作为椭圆和双曲线的离心率.
的两根可分别作为椭圆和双曲线的离心率.
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案