题目内容
(本小题14分)已知直线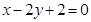 经过椭圆
经过椭圆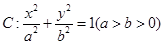 的左顶点
的左顶点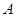 和上顶点
和上顶点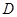 ,椭圆
,椭圆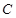 的右顶点为
的右顶点为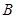 ,点
,点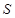 是椭圆
是椭圆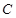 上位于
上位于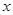 轴上方的动点,直线
轴上方的动点,直线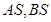 与直线
与直线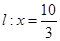 分别交于
分别交于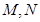 两点.
两点.
(1)求椭圆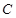 的方程;
的方程;
(2)求证:直线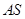 与直线
与直线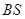 斜率
斜率 的乘积为定值;
的乘积为定值;
(3)求线段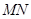 的长度的最小值.
的长度的最小值.
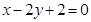 经过椭圆
经过椭圆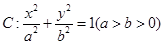 的左顶点
的左顶点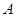 和上顶点
和上顶点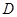 ,椭圆
,椭圆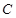 的右顶点为
的右顶点为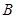 ,点
,点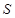 是椭圆
是椭圆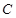 上位于
上位于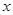 轴上方的动点,直线
轴上方的动点,直线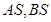 与直线
与直线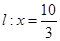 分别交于
分别交于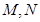 两点.
两点.(1)求椭圆
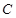 的方程;
的方程; (2)求证:直线
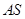 与直线
与直线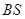 斜率
斜率 的乘积为定值;
的乘积为定值;(3)求线段
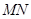 的长度的最小值.
的长度的最小值.(1)由已知得,椭圆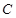 的左顶点为
的左顶点为 上顶点为
上顶点为
故椭圆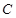 的方程为
的方程为 ……………………………4分
……………………………4分
(2)设直线AS的斜率 ,直线BS的斜率
,直线BS的斜率 的乘积为
的乘积为
 =
= ………………..8分
………………..8分
(3)解法一:直线AS的斜率 显然存在,且
显然存在,且 >0,故可设直线
>0,故可设直线 的方程为
的方程为 ,
,
从而 由(2)知直线BS的方程为
由(2)知直线BS的方程为
从而 ,
,

 ,当且仅当
,当且仅当 ,即
,即 时等号成立
时等号成立
线段 的长度取最小值
的长度取最小值 ……………………………………………14分
……………………………………………14分
解法二:直线AS的斜率 显然存在,且
显然存在,且 ,故可设直线
,故可设直线 的方程为
的方程为 ,
,
从而 由
由 得
得 0
0
设 则
则 得
得 ,从而
,从而
即 又
又 由
由 得
得

故 又
又 当且仅当
当且仅当 ,即
,即 时等号成立
时等号成立
 时,线段
时,线段 的长度取最小值
的长度取最小值 ………………………14分
………………………14分
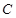 的左顶点为
的左顶点为 上顶点为
上顶点为
故椭圆
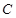 的方程为
的方程为 ……………………………4分
……………………………4分(2)设直线AS的斜率
 ,直线BS的斜率
,直线BS的斜率 的乘积为
的乘积为
 =
= ………………..8分
………………..8分(3)解法一:直线AS的斜率
 显然存在,且
显然存在,且 >0,故可设直线
>0,故可设直线 的方程为
的方程为 ,
,从而
 由(2)知直线BS的方程为
由(2)知直线BS的方程为
从而
 ,
,

 ,当且仅当
,当且仅当 ,即
,即 时等号成立
时等号成立线段
 的长度取最小值
的长度取最小值 ……………………………………………14分
……………………………………………14分解法二:直线AS的斜率
 显然存在,且
显然存在,且 ,故可设直线
,故可设直线 的方程为
的方程为 ,
,从而
 由
由 得
得 0
0 设
 则
则 得
得 ,从而
,从而
即
 又
又 由
由 得
得

故
 又
又 当且仅当
当且仅当 ,即
,即 时等号成立
时等号成立 时,线段
时,线段 的长度取最小值
的长度取最小值 ………………………14分
………………………14分略

练习册系列答案
相关题目
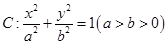 的左、右焦点分别为
的左、右焦点分别为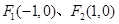 ,且经过定点
,且经过定点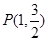 ,
,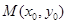 为椭圆
为椭圆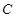 上的动点,以点
上的动点,以点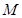 为圆心,
为圆心,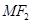 为半径作圆
为半径作圆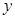 轴有两个不同交点,求点
轴有两个不同交点,求点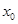 的取值范围;
的取值范围;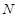 ,使得圆
,使得圆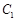 :
: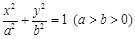 的离心率为
的离心率为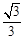 ,直线
,直线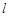 :
: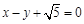 与椭圆
与椭圆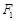 ,右焦点为
,右焦点为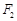 ,直线
,直线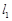 过点
过点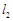 垂直于直线
垂直于直线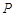 ,线段
,线段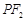 的垂直平分线交
的垂直平分线交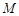 ,求点
,求点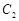 的方程.
的方程.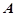 和
和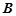 ,且
,且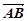 与
与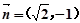 共线.
共线.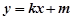 与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.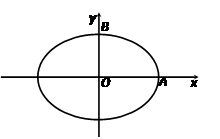
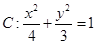 的左焦点
的左焦点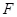 作倾斜角为
作倾斜角为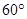 的直线
的直线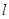 与椭圆
与椭圆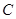 交于
交于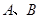 两点,则
两点,则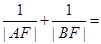 ( )
( )



 的焦点
的焦点 为椭圆上的一点,已知
为椭圆上的一点,已知 ,则
,则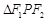 的面积为( )
的面积为( ) 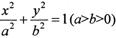 的左、右焦点分别为
的左、右焦点分别为 ,离心率
,离心率 ,A为右顶点,K为右准线与X轴的交点,且
,A为右顶点,K为右准线与X轴的交点,且 .
.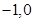 ),F2(1,0),直线x = 4是椭圆的一条准线.
),F2(1,0),直线x = 4是椭圆的一条准线.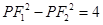 ,求cos∠F1PF2的值;
,求cos∠F1PF2的值;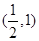 是椭圆内一点,在椭圆上求一点Q,使得
是椭圆内一点,在椭圆上求一点Q,使得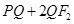 最小.
最小.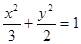 的离心率
的离心率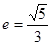 ,长轴长为
,长轴长为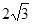 ;②抛物线
;②抛物线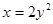 的准线方程为
的准线方程为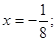 ③双曲线
③双曲线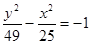 的渐近线方程为
的渐近线方程为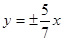 ;④方程
;④方程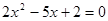 的两根可分别作为椭圆和双曲线的离心率.
的两根可分别作为椭圆和双曲线的离心率.