题目内容
(本小题满分12分)
已知椭圆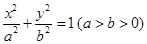 的长轴长为
的长轴长为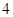 ,且点
,且点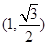 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)过椭圆右焦点的直线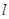 交椭圆于
交椭圆于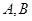 两点,若以
两点,若以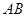 为直径的圆过原点,
为直径的圆过原点,
求直线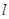 方程.
方程.
已知椭圆
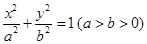 的长轴长为
的长轴长为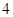 ,且点
,且点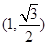 在椭圆上.
在椭圆上.(Ⅰ)求椭圆的方程;
(Ⅱ)过椭圆右焦点的直线
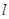 交椭圆于
交椭圆于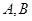 两点,若以
两点,若以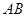 为直径的圆过原点,
为直径的圆过原点,求直线
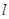 方程.
方程.解:(Ⅰ)由题意: ,
, .所求椭圆方程为
.所求椭圆方程为 .
.
又点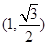 在椭圆上,可得
在椭圆上,可得 .所求椭圆方程为
.所求椭圆方程为 . …4分
. …4分
(Ⅱ)由(Ⅰ)知 ,所以
,所以 ,椭圆右焦点为
,椭圆右焦点为 .
.
因为以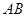 为直径的圆过原点,所以
为直径的圆过原点,所以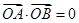 .
.
若直线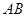 的斜率不存在,则直线
的斜率不存在,则直线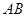 的方程为
的方程为 .
.
直线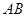 交椭圆于
交椭圆于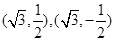 两点,
两点,  ,不合题意.
,不合题意.
若直线 的斜率存在,设斜率为
的斜率存在,设斜率为 ,则直线
,则直线 的方程为
的方程为 .
.
由 可得
可得 .
.
由于直线 过椭圆右焦点,可知
过椭圆右焦点,可知 .
.
设 ,则
,则 ,
,
 .
.
所以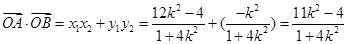 .
.
由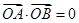 ,即
,即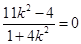 ,可得
,可得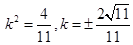 .
.
所以直线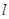 方程为
方程为 . ………………12分
. ………………12分
 ,
, .所求椭圆方程为
.所求椭圆方程为 .
.又点
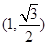 在椭圆上,可得
在椭圆上,可得 .所求椭圆方程为
.所求椭圆方程为 . …4分
. …4分(Ⅱ)由(Ⅰ)知
 ,所以
,所以 ,椭圆右焦点为
,椭圆右焦点为 .
.因为以
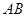 为直径的圆过原点,所以
为直径的圆过原点,所以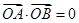 .
.若直线
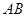 的斜率不存在,则直线
的斜率不存在,则直线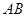 的方程为
的方程为 .
.直线
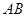 交椭圆于
交椭圆于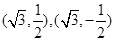 两点,
两点,  ,不合题意.
,不合题意.若直线
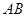 的斜率存在,设斜率为
的斜率存在,设斜率为 ,则直线
,则直线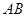 的方程为
的方程为 .
.由
 可得
可得 .
.由于直线
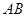 过椭圆右焦点,可知
过椭圆右焦点,可知 .
.设
 ,则
,则 ,
, .
.所以
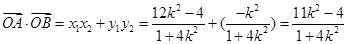 .
.由
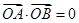 ,即
,即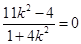 ,可得
,可得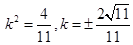 .
.所以直线
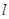 方程为
方程为 . ………………12分
. ………………12分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
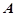 和
和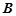 ,且
,且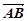 与
与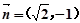 共线.
共线.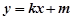 与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
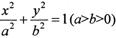 的左、右焦点分别为
的左、右焦点分别为 ,离心率
,离心率 ,A为右顶点,K为右准线与X轴的交点,且
,A为右顶点,K为右准线与X轴的交点,且 .
. 、
、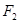 分别是椭圆
分别是椭圆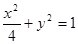 的左、右焦点.
的左、右焦点.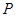 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求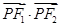 的最大值和最小值;
的最大值和最小值;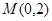 的直线
的直线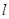 与椭圆交于不同的两点
与椭圆交于不同的两点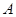 、
、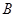 ,且∠
,且∠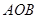 为锐角(其中
为锐角(其中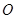 为坐标原点),求直线
为坐标原点),求直线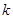 的取值范围.
的取值范围.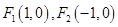 ,过
,过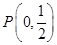 作垂直于
作垂直于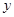 轴的直线被椭圆所截线段长为
轴的直线被椭圆所截线段长为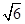 ,过
,过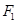 作直线l与椭圆交于A、B两点.
作直线l与椭圆交于A、B两点.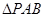 的面积;
的面积;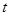 使
使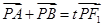 ,若存在,求
,若存在,求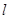 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.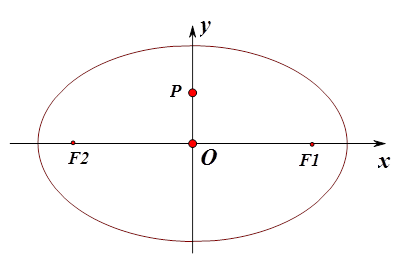
 是椭圆
是椭圆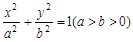 上的一动点,且
上的一动点,且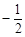 ,则椭圆离心率为 ( )
,则椭圆离心率为 ( )



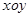 中,向量
中,向量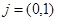 ,△OFP的面积为
,△OFP的面积为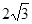 ,且
,且
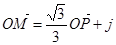 。
。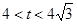 ,求向量
,求向量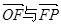 的夹角
的夹角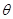 的取值范围;
的取值范围;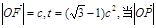 取最小值时,求椭圆的方程。
取最小值时,求椭圆的方程。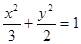 的离心率
的离心率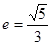 ,长轴长为
,长轴长为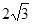 ;②抛物线
;②抛物线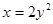 的准线方程为
的准线方程为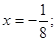 ③双曲线
③双曲线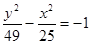 的渐近线方程为
的渐近线方程为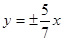 ;④方程
;④方程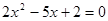 的两根可分别作为椭圆和双曲线的离心率.
的两根可分别作为椭圆和双曲线的离心率.