Question

【题目】已知函数，若关于的方程恰有三个不相等的实数解，则的取值范围是　　

A. B.

C. D.

Answer 1

【答案】B

【解析】

设，则是的图象沿着上下平移得到，分析函数与的图象，利用图象关系确定两个函数满足的条件进行求解即可．

设，

则是的图象沿着上下平移得到，

当x=1时，（1）（1），

所以直线x=1与函数h(x)的图像的交点坐标为（1，m）,

当x=1时，g(1)=0,

当x=2时，（2），所以直线x=2与函数g(x)的图像的交点为（2，-2），

当x=2时，（2），所以直线x=2与函数h(x)的图像的交点为（2，ln2+m）,

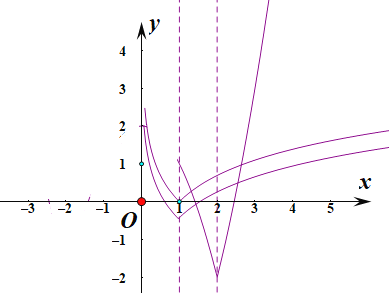
要使方程恰有三个不相等的实数解，

则等价为与的图象有三个不同的交点，

则满足，

即得，

即，

即实数的取值范围是，，

故选：．