题目内容
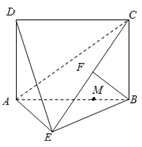
【题目】如图,已知长方形![]() 中,
中, ![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
(1)求证: ![]() ;
;
(2)设![]() ,当
,当![]() 为何值时,二面角
为何值时,二面角![]() 的余弦值
的余弦值![]() .
.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)设![]() ,
, ![]() 为
为![]() 的中点,得
的中点,得![]() ,进而得
,进而得![]() 平面
平面![]() ,即可得到
,即可得到![]() .
.
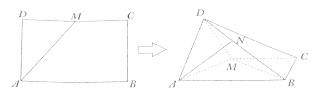
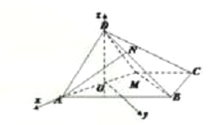
(2)取![]() 的中点
的中点![]() ,以
,以![]() 为坐标原点,建立如图所示的直角坐标系,求得平面
为坐标原点,建立如图所示的直角坐标系,求得平面![]() 的一个法向量为
的一个法向量为![]() 和平面
和平面![]() 的一个法向量
的一个法向量![]() ,即可利用向量的夹角公式,即得到二面角的余弦值.
,即可利用向量的夹角公式,即得到二面角的余弦值.
试题解析:
(1)证明:因为长方形![]() 中,设
中,设![]() ,
, ![]() 为
为![]() 的中点,
的中点,
所以![]() ,所以
,所以![]() ,因为平面
,因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)取![]() 的中点
的中点![]() ,以
,以![]() 为坐标原点,因为
为坐标原点,因为![]() 平面
平面![]() ,
,
建立如图所示的直角坐标系,则平面![]() 的一个法向量
的一个法向量![]() ,
, ![]() ,
,
由![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,联立
,联立![]() ,取
,取![]() ,
,
得![]() ,所以
,所以![]() ,
,
因为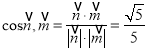 ,求得
,求得![]() ,所以
,所以![]() 为
为![]() 的中点,
的中点,
故点![]() 时,二面角
时,二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】2018年2月25日第23届冬季奥运会在韩国平昌闭幕,中国以1金6银2铜的成绩结束本次冬奥会的征程.某校体育爱好者协会在高三年级某班进行了“本届冬奥会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),按分层抽样从被调查的学生中随机抽取了11人,具体的调查结果如下表:
某班 | 满意 | 不满意 |
男生 | 2 | 3 |
女生 | 4 | 2 |
(Ⅰ)若该班女生人数比男生人数多4人,求该班男生人数和女生人数
(Ⅱ)在该班全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(Ⅲ)若从该班调查对象中随机选取2人进行追踪调查,记选中的2人中对“本届冬奥会中国队表现”满意的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.