题目内容
(本题满分12分)
已知函数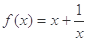
⑴求证: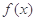 在
在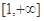 上是增函数;
上是增函数;
⑵求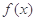 在
在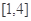 上的最大值及最小值。
上的最大值及最小值。
已知函数
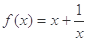
⑴求证:
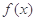 在
在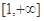 上是增函数;
上是增函数;⑵求
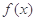 在
在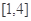 上的最大值及最小值。
上的最大值及最小值。证明:⑴见解析;
⑵当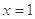 时,
时,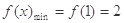 ,当
,当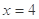 时,
时,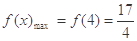 。
。
⑵当
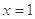 时,
时,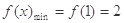 ,当
,当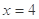 时,
时,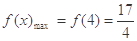 。
。本试题主要是考查了函数单调性的证明以及函数的最值的求解。
(1)利用定义法,设出变量,作差,变形,定号,下结论。
(2)根据第一问的结论,那么可知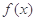 在
在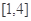 上递增,当
上递增,当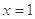 时,
时,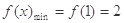
当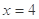 时,
时,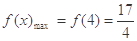
证明:⑴任取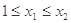 ,则
,则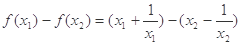 =
=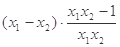
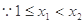
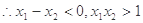
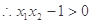
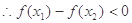
即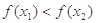
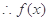 在
在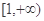 上是增函数
上是增函数
解⑵由⑴可知,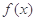 在
在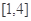 上递增,当
上递增,当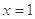 时,
时,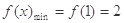
当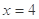 时,
时,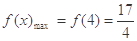
(1)利用定义法,设出变量,作差,变形,定号,下结论。
(2)根据第一问的结论,那么可知
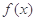 在
在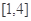 上递增,当
上递增,当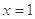 时,
时,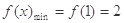
当
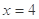 时,
时,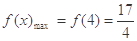
证明:⑴任取
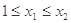 ,则
,则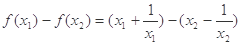 =
=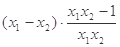
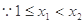
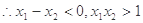
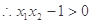
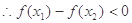
即
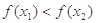
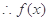 在
在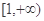 上是增函数
上是增函数解⑵由⑴可知,
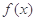 在
在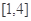 上递增,当
上递增,当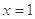 时,
时,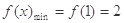
当
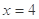 时,
时,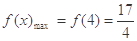

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
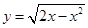 的单调递减区间是 __________________.
的单调递减区间是 __________________.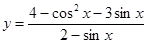 的最大值是( )
的最大值是( )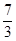
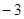
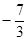
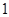
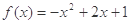
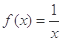
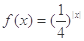
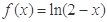
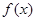 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,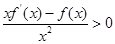 ,且
,且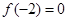 ,则不等式
,则不等式 的解集是( )
的解集是( )  ∪
∪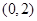
 ∪
∪
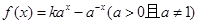 是定义域为R的奇函数.
是定义域为R的奇函数.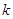 的值;
的值;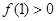 ,试判断函数单调性(不需证明)并求不等式
,试判断函数单调性(不需证明)并求不等式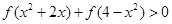 的解集;
的解集;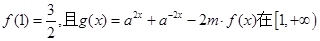 上的最小值为
上的最小值为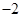 ,求
,求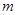 的值.
的值. 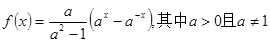
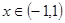 时,有
时,有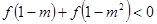 ,求
,求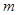 的取值范围.
的取值范围.  ,则使
,则使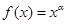 为奇函数且在
为奇函数且在 单调递减的
单调递减的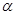 的值的个数是( )
的值的个数是( )