题目内容
4.(Ⅰ) 数列{an}满足Sn=2n-an,先计算数列的前四项,再归纳猜想通项an;(Ⅱ) 用分析法证明:$\sqrt{6}+\sqrt{7}>2\sqrt{2}+\sqrt{5}$.
分析 (Ⅰ)根据Sn=2n-an,利用递推公式,求出a1,a2,a3,a4.总结出规律求出an;
(Ⅱ)寻找使不等式成立的充分条件,要是不等式成立,只要6+7+2$\sqrt{42}$>8+5+4$\sqrt{10}$,即证$\sqrt{42}$>2$\sqrt{10}$,即证 42>40.
解答 (Ⅰ)解:由a1=2-a1,得a1=1,
由a1+a2=2×2-a2,得a2=$\frac{3}{2}$,
由a1+a2+a3=2×3-a3,得a3=$\frac{7}{4}$,
由a1+a2+a3+a4=2×4-a4,得a4=$\frac{15}{8}$,
猜想an=$\frac{{2}^{n}-1}{{2}^{n-1}}$;
(Ⅱ)证明:要证$\sqrt{6}+\sqrt{7}>2\sqrt{2}+\sqrt{5}$,
只要证 6+7+2$\sqrt{42}$>8+5+4$\sqrt{10}$,
只要证$\sqrt{42}$>2$\sqrt{10}$,即证 42>40.
而42>40显然成立,故原不等式成立.
点评 本题考查归纳猜想,考查用分析法证明不等式,关键是寻找使不等式成立的充分条件.

练习册系列答案
相关题目
14.已知数列{an}满足a1=2,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$(n∈N*),则a1a2a3…a2012的值为( )
| A. | 2 | B. | -3 | C. | $-\frac{1}{2}$ | D. | 1 |
15.已知定义在R上的函数f(x)是奇函数,且f(2)=0,当x>0时有x•f′(x)+f(x)<0,则不等式f(x)<0的解集是( )
| A. | (-2,0)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-2,2)∪(2,+∞) |
19.函数y=x3+x的递增区间是( )
| A. | (0,+∞) | B. | (-∞,1) | C. | (1,+∞) | D. | (-∞,+∞) |
16.命题“?x∈R,x2+x+1>0”的否定为( )
| A. | ?x∈R,x2+x+1≤0 | B. | ?x∉R,x2+x+1≤0 | ||
| C. | ?x0∉R,x02+x0+1>0 | D. | ?x0∈R,x02+x0+1≤0 |
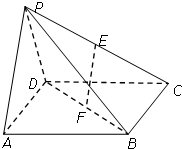 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a. 我校要对高一学生的数学成绩进行调查,现从中随机抽出若干名学生的数学成绩进行分析,绘制频率分布直方图如图,若低于60分的人数是15,
我校要对高一学生的数学成绩进行调查,现从中随机抽出若干名学生的数学成绩进行分析,绘制频率分布直方图如图,若低于60分的人数是15,