题目内容
9.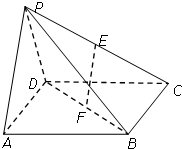 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a.(1)求证:EF∥平面PAD;
(2)求三棱锥E-PBD的体积.
分析 (1)连接AC,则F是AC的中点,E为PC的中点,要证EF∥平面PAD,只需证明EF∥PA即可;
(2)求三棱锥C-PBD的体积,转化为P-BCD的体积,求出底面面积和高,即可求出三棱锥E-PBD的体积.
解答 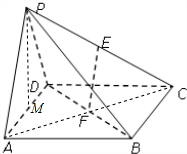 (1)证明:连接AC,则F是AC的中点,E为PC的中点
(1)证明:连接AC,则F是AC的中点,E为PC的中点
故在△CPA中,EF∥PA,(3分)
且PA?平面PAD,EF?平面PAD,
∴EF∥平面PAD(6分)
(2)解:取AD的中点M,连接PM,
∵PA=PD,
∴PM⊥AD(8分)
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PM⊥平面ABCD,(10分)
∴三棱锥E-PBD的体积=$\frac{1}{2}{V}_{C-PBD}=\frac{1}{2}{V}_{P-BCD}$=$\frac{1}{3}{S}_{△BCD}•PM$=$\frac{1}{2}•\frac{1}{3}•\frac{1}{2}a•a•\frac{1}{2}a$=$\frac{{a}^{3}}{24}$.(14分)
点评 本题考查直线和平面平行的判定,棱锥的体积,考查平面与平面垂直的性质,是中档题.

练习册系列答案
相关题目
19.把极坐标系下的点坐标(4,$\frac{π}{4}$)化为直角坐标系下的点坐标为( )
| A. | (2,2$\sqrt{2}$) | B. | (2$\sqrt{2}$,2) | C. | (2$\sqrt{2}$,2$\sqrt{2}$) | D. | (1,0) |
17.i为虚数单位,则(1-i)2的虚部为( )
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |
18.已知点P在曲线y=x3-x+$\frac{2}{3}$上移动,设点P处切线的倾斜角为α,则α的取值范围是( )
| A. | [0,$\frac{π}{2}$] | B. | [0,$\frac{π}{2}$]∪(-$\frac{π}{2}$,0) | C. | [$\frac{3π}{4}$,π] | D. | [0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π) |
19.将点(2,3)变成点(3,2)的伸缩变换是( )
| A. | $\left\{\begin{array}{l}x'=\frac{2}{3}x\\ y'=\frac{3}{2}y\end{array}\right.$ | B. | $\left\{\begin{array}{l}x'=\frac{3}{2}x\\ y'=\frac{2}{3}y\end{array}\right.$ | C. | $\left\{\begin{array}{l}x'=y\\ y'=x\end{array}\right.$ | D. | $\left\{\begin{array}{l}x'=x+1\\ y'=y-1\end{array}\right.$ |