Question

【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关，现对30名六年级学生进行了问卷调查得到如下列联表：

	常喝	不常喝	合计
肥胖		2
不肥胖		18
合计			30

已知在全部30人中随机抽取1人，抽到肥胖的学生的概率为．

（1）请将上面的列表补充完整；

（2）是否有99.5%的把握认为肥胖与常喝碳酸饮料有关？说明你的理由；

（3）4名调查人员随机分成两组，每组2人，一组负责问卷调查，另一组负责数据处理，求工作人员甲分到负责收集数据组，工作人员乙分到负责数据处理组的概率．

参考数据：

	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式： ）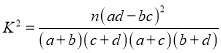

Answer 1

【答案】（1）表格祥见解析；（2）有，理由祥见解析；（3）.

【解析】试题分析：（1）根据全部50人中随机抽取1人看营养说明的学生的概率为，做出看营养说明的人数，这样用总人数减去看营养说明的人数，剩下的是不看的，根据所给的另外两个数字，填上所有数字．

（2）根据列联表所给的数据，代入求观测值的公式，把观测值同临界值进行比较，得到有99.5%的把握说看营养说明与性别有关．

（3）利用列举法，求出基本事件的个数，即可求出正好抽到一男一女的概率．

试题解析：（1）设常喝碳酸饮料肥胖的学生有人， ，

	常喝	不常喝	合计
肥胖	6	2	8
不胖	4	18	22
合计	10	20	30

（2）由已知数据可求得： ，

因此有99.5%的把握认为肥胖与常喝碳酸饮料有关．

（3）设其他工作人员为丙和丁，4人分组的所有情况如下表

小组	1	2	3	4	5	6
收集数据	甲乙	甲丙	甲丁	乙丙	乙丁	丙丁
处理数据	丙丁	乙丁	乙丙	甲丁	甲丙	甲乙

分组的情况总有6中，工作人员甲 负责收集数据且工作人员乙负责处理数据占两种，

所以工作人员甲负责收集数据且工作人员处理数据的概率是．