题目内容
8.三棱锥P-ABC中,PA=PB=PC=AB=AC=1,∠BAC=90°,则PA与底面ABC所成角的大小为45°.分析 取BC的中点E,根据三角形的边长关系证明∠PAE是PA与底面ABC所成的角即可.
解答 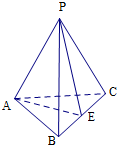 解:∵AB=AC=1,∠BAC=90°,
解:∵AB=AC=1,∠BAC=90°,
∴BC=$\sqrt{2}$,
∵PB=PC=1,∴∠BPC=90°,
取BC的中点E,
则PE=AE=$\sqrt{2}$,
∵PA=1,
∴∠PEA=90°,
则∠PAE=45°,
∵E是BC的中点,
∴PE⊥BC,AE⊥BC,
∴BC⊥平面ABC,
则∠PAE是PA与底面ABC所成的角,
即PA与底面ABC所成角的大小为45°.
故答案为:45°
点评 本题主要考查直线和平面所成角的大小的求解,根据定义确定线面角是解决本题的关键.

练习册系列答案
相关题目
11.数列{an}中,an=$\frac{n-\sqrt{2012}}{n-\sqrt{2013}}$,则该数列前100项中的最大项与最小项分别是( )
(参考数据:442=1936,452=2045)
(参考数据:442=1936,452=2045)
| A. | a1,a50 | B. | a1,a44 | C. | a45,a44 | D. | a45,a50 |
17.若函数f(x)=$\frac{1}{n}{e^{mx}}$(m,n∈R+)的图象在x=0处的切线l与圆C:x2+y2=1相切,则m+n的最大值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
18.已知抛物线y2=2px(p>0)与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)有相同的焦点F,若点A是抛物线与双曲线的一个交点,且AF⊥x轴,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}+1}{2}$ | B. | $\sqrt{2}$+1 | C. | $\sqrt{3}$+1 | D. | $\frac{2\sqrt{2}+1}{2}$ |