题目内容
8.二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(-1,0).设t=a+b+1,则t值的变化范围是( )| A. | 0<t<1 | B. | 0<t<2 | C. | 1<t<2 | D. | -1<t<1 |
分析 由二次函数的解析式可知,当x=1时,y=a+b+1=t,根据图象的顶点在第一象限,且过点(-1,0)画出草图,求a,b的范围,问题得以解决.
解答 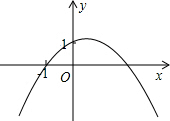 解:∵二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(-1,0),
解:∵二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(-1,0),
∴易得a-b+1=0,a<0,b>0,
由a=b-1<0,得到b<1,结合上面得到b>0,所以0<b<1①,
由b=a+1>0,得到a>-1,结合上面得到a<0,所以-1<a<0②,
∴由①+②得:-1<a+b<1,
∴0<a+b<2,
∵t=a+b+1,
∴0<t<2,
故选:B.
点评 本题考查了二次函数图象与根与系数的关系,在解题时要结合二次函数的图象和系数,对称轴,特殊点,属于基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
18.已知f(x)是定义在R上的周期为2的奇函数,当x∈(0,1)时,f(x)=3x-1,则f($\frac{2015}{2}$)=( )
| A. | $\sqrt{3}$+1 | B. | -$\sqrt{3}$+1 | C. | $\sqrt{3}$-1 | D. | -$\sqrt{3}$-1 |
16.如图为某几何体的三视图,图中四边形为边长为1的正方形,两条虚线互相垂直,则该几何体体积为( )


| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |
3.已知点A=(-1,1)、B=(1,2)、C=(-3,2),则向量$\overrightarrow{AB}$在$\overrightarrow{AC}$方向上的投影为( )
| A. | -$\frac{3}{5}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | -$\frac{3\sqrt{5}}{5}$ | D. | $\frac{3}{5}$ |
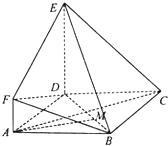 如图,四边形ABCD是菱形,DE⊥DC,平面DEC⊥平面ABCD.
如图,四边形ABCD是菱形,DE⊥DC,平面DEC⊥平面ABCD.