题目内容
5.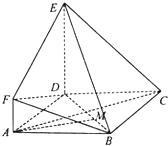 如图,四边形ABCD是菱形,DE⊥DC,平面DEC⊥平面ABCD.
如图,四边形ABCD是菱形,DE⊥DC,平面DEC⊥平面ABCD.(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)若AF∥DE,AF=$\frac{1}{3}$DE,点M在线段BD上,且DM=$\frac{2}{3}$BD,求证:AM∥平面BEF.
分析 (Ⅰ)由空间中的垂直关系以及菱形的对角线互相垂直,证出AC⊥平面BDE;
(Ⅱ)证法一,延长EF,DA,交于点G,证明AM∥GB即可;
证法二,在△EDB中,过点M作MN∥DE,MN∩BE=N,连接FN,证明四边形AMNF为平行四边形,得AM∥FN即可.
解答 证明:(Ⅰ)因为平面DEC⊥平面ABCD,
DE⊥DC,平面DEC∩平面ABCD=DC,
DE?平面DEC,
所以DE⊥平面ABCD,
又AC?平面ABCD,
所以DE⊥AC,
因为ABCD是菱形,
所以AC⊥BD,
又BD∩DE=D,
BD、DE?平面BDE,
∴AC⊥平面BDE;
(Ⅱ)如图所示,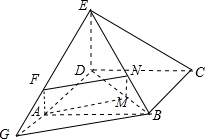
证法一,延长EF,DA,交于点G,
因为AF∥DE,AF=$\frac{1}{3}$DE,
所以$\frac{GA}{GD}$=$\frac{AF}{DE}$=$\frac{1}{3}$,
因为DM=$\frac{2}{3}$BD,所以BM=$\frac{1}{3}$BD,
因此$\frac{BM}{BD}$=$\frac{1}{3}$,所以$\frac{BM}{BD}$=$\frac{GA}{GD}$=$\frac{1}{3}$,
所以AM∥GB,
又AM?平面BEF,GB?平面PEF,
所以AM∥平面PEF.
证法二,在△EDB中,过点M作MN∥DE,MN∩BE=N,
连接FN,
因为AF∥DE,
所以MN∥AF,
因为DM=$\frac{2}{3}$BD,所以BM=$\frac{1}{3}$BD,
$\frac{MN}{DE}$=$\frac{BM}{BD}$=$\frac{1}{3}$,
又$\frac{AF}{DE}$=$\frac{1}{3}$,
所以MN=AF,
所以四边形AMNF为平行四边形,
所以AM∥FN,
因为AM?平面BEF,
所以AM∥平面BEF.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了空间想象能力与逻辑思维能力的应用问题,是综合性题目.

| A. | 0<t<1 | B. | 0<t<2 | C. | 1<t<2 | D. | -1<t<1 |
| A. | 原命题为真,否命题为假 | B. | 原命题为假,否命题为真 | ||
| C. | 原命题与否命题均为真命题 | D. | 原命题与否命题均为假命题 |
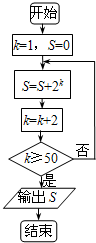
| A. | $\frac{2}{3}({4^{25}}-1)$ | B. | $\frac{2}{3}({4^{26}}-1)$ | C. | 250-1 | D. | 251-1 |
| A. | $\sqrt{5}$ | B. | -2$\sqrt{5}$ | C. | 4 | D. | -4 |
甲养猪场猪重频数分布表
| 猪的重量分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 8 | 20 | 42 | 22 | 8 |
| 猪的重量分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 4 | 12 | 42 | 32 | 10 |
(Ⅱ)已知乙养猪场出栏一头猪的利润y(单位:百元)与其重量x(单位:公斤)的关系为:y=$\left\{\begin{array}{l}{-2(x<94)}\\{2(94≤x<102)}\\{4(x≥102)}\end{array}\right.$估计乙养猪场平均每出栏一头猪的利润.
 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1上的动点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1上的动点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.