题目内容
13.掷骰子2次,每个结果以(x,y)记之,其中x1,x2分别表示第一颗,第二颗骰子的点数,设A={(x1,x2)|x1+x2=10},B={(x1,x2)|x1>x2},则P(B|A)=$\frac{1}{3}$.分析 A可能为(4,6),(6,4),(5,5),B为(6,4),即可求出P(B|A).
解答 解:A可能为(4,6),(6,4),(5,5),B为(6,4),
所以P(B|A)=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查条件概率,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
3.若某几何体的三视图如图所示,则此几何体的侧面积是( )


| A. | 12π | B. | 15π | C. | 24π | D. | 30π |
4.执行如图所示的程序框图,则输出的结果是( )


| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | -1 |
8.二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(-1,0).设t=a+b+1,则t值的变化范围是( )
| A. | 0<t<1 | B. | 0<t<2 | C. | 1<t<2 | D. | -1<t<1 |
9.已知某高级中学高三学生有2000名,在第一次模拟考试中数学成绩ξ服从正态分布N(120,σ2),已知P(100<?<120)=0.45.若学校教研室欲按分层抽样的方式从中抽出100份试卷进行分析研究,则应从140分以上的试卷中抽( )
| A. | 4份 | B. | 5份 | C. | 8份 | D. | 10份 |
10.执行如图所示的程序框图,输出的S值为( )
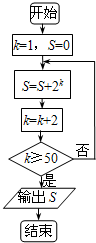

| A. | $\frac{2}{3}({4^{25}}-1)$ | B. | $\frac{2}{3}({4^{26}}-1)$ | C. | 250-1 | D. | 251-1 |
 如图,在棱长为1的正四面体A-BCD中,平面α与棱AB,AD,CD,BC分别交于点E,F,G,H,则四边形EFGH周长的最小值为2.
如图,在棱长为1的正四面体A-BCD中,平面α与棱AB,AD,CD,BC分别交于点E,F,G,H,则四边形EFGH周长的最小值为2.