Question

18．已知正四面体棱长为a，求正四面体内切球体积．

Answer 1

分析 作出正四面体的图形，确定球的球心位置为O，说明OE是内切球的半径，运用勾股定理计算，即可得到球的体积．

解答 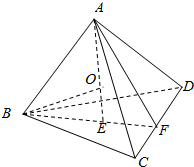解：如图O为正四面体ABCD的内切球的球心，
正四面体的棱长为a，OE为内切球的半径，设OA=OB=R，
在等边三角形BCD中，BE=$\frac{\sqrt{3}}{3}$a，
AE=$\sqrt{{a}^{2}-\frac{1}{3}{a}^{2}}$=$\frac{\sqrt{6}}{3}$a．
由OB²=OE²+BE²，即有R²=（$\frac{\sqrt{6}}{3}$a-R）²+（$\frac{\sqrt{3}}{3}$a）²，
解得，R=$\frac{\sqrt{6}}{4}$a．OE=AE-R=$\frac{\sqrt{6}}{12}$a，
则其内切球的半径是$\frac{\sqrt{6}}{12}$a，
内切球的体积为$\frac{4}{3}$π×（$\frac{\sqrt{6}}{12}$a）³=$\frac{\sqrt{6}}{216}π{a}^{3}$．

点评 本题考查正四面体的内切球半径的求法，内切球的半径是正四面体的高的$\frac{1}{4}$，是中档题，解题时要认真审题，注意空间思维能力的培养．