题目内容
7．己知圆C：（x-2）2+（y-4）2=1．P（x，y）为圆C上一点，则x2+y2的取值范围是[21-4$\sqrt{5}$，21+4$\sqrt{5}$]．分析 找出圆心与半径，所求式子表示圆上点到原点距离的平方，从而求x2+y2的取值范围；
解答 解：圆C：（x-2）2+（y-4）2=1．圆心为（2，4），半径为1．圆心到原点的距离为：$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{20}$
=$2\sqrt{5}$，
x2+y2的最大值为：$（2\sqrt{5}+1）^{2}$=21+4$\sqrt{5}$．
x2+y2的最小值为：${（2\sqrt{5}-1）}^{2}$=21-4$\sqrt{5}$．
∴x2+y2的取值范围是[21-4$\sqrt{5}$，21+4$\sqrt{5}$]；
故答案为：[21-4$\sqrt{5}$，21+4$\sqrt{5}$]；
点评 本小题主要考查直线和圆的综合应用，考查数形结合、化归转化的数学思想方法，以及推理论证能力、运算求解能力，属于中档题．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
17．设a=log43，b=30.4，c=log3$\frac{1}{4}$，则（ ）
| A． | b＞a＞c | B． | a＞c＞b | C． | c＞a＞b | D． | a＞b＞c |
15．若等差数列的第一、二、三项依次是$\frac{1}{x+1}$、$\frac{5}{6x}$、$\frac{1}{x}$则数列的公差d是（ ）
| A． | $\frac{1}{12}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
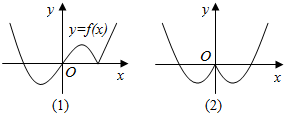已知如图（1）的图象对应的函数为y=f（x），给出①y=f（|x|）；②y=|f（x）|-a；③y=-f（|x|）；④y=f（-|x|）．⑤y=|f（|x|）|-a，则如图（2）的图象对应的函数可能是五个式子中的（ ）