题目内容
8．三棱锥P-ABC中，（1）若点P到AB，BC，CA的距离相等，那么点P在底面内的射影是△ABC的内心或旁心；
（2）若两组对棱互相垂直，那么点P在底面内的射影是△ABC的垂心．
分析 （1）根据题意得出点P在平面ABC内的射影到三边的距离相等，是内心或旁心；
（2）根据题意得出点P在底面ABC内的射影O是△ABC的垂心．
解答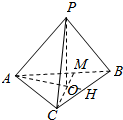 
解：三棱锥P-ABC中，
（1）点P到AB，BC，CA的距离相等，则点P在平面ABC内的射影到三边的距离也相等，
到三角形三边距离相等的点是三角形的内心或是旁心，
所以点P在底面的射影是△ABC的内心或旁心；
（2）若两组对棱互相垂直，如图所示，
PA⊥BC，PC⊥AD，
容易得出AH⊥BC，CM⊥AB，
所以点P在底面ABC内的射影O是△ABC的垂心．
故答案为：（1）内心或旁；（2）垂．
点评 本题考查了三角形五心的概念及线线垂直判断问题，因为旁心和内心都符合到三角形三边距离相等的条件，我们的教学中只注重内心问题，是综合题目．
练习册系列答案
阅读快车系列答案
相关题目
18．存在函数f（x）满足，对于任意x∈R都有（ ）
| A． | f（x2）=x | B． | f（x2+x）=x+3 | C． | f（|log2x|）=x2+x | D． | f（x2+2x）=|x+1| |
19．已知f（x）=$\left\{\begin{array}{l}{{x}^{2}+1（x＜1）}\\{-2x+3（x≥1）}\end{array}\right.$，则f（f（2））=（ ）
| A． | -7 | B． | 2 | C． | -1 | D． | 5 |
3．方程（x2-4）2+$\sqrt{{y}^{2}-4}$=0表示的图形是（ ）
| A． | 两条直线 | B． | 两个点 | C． | 四个点 | D． | 四条直线 |
17．设a=log43，b=30.4，c=log3$\frac{1}{4}$，则（ ）
| A． | b＞a＞c | B． | a＞c＞b | C． | c＞a＞b | D． | a＞b＞c |