题目内容
9.已知各项均为正数的数列{an}的前n项和为Sn,且a${\;}_{n}^{2}+{a}_{n}$=2Sn.(1)求数列{an}的通项;
(2)若bn=$\frac{1}{{a}_{n}^{2}}$(n∈N+),Tn=b1+b2+…+bn,求证:Tn$<\frac{5}{3}$.
分析 (1)a${\;}_{n}^{2}+{a}_{n}$=2Sn,利用递推关系化为(an+1+an)(an+1-an-1)=0,可得an+1-an=1.利用等差数列的通项公式即可得出.
(2)n=1时,b1=$\frac{1}{{a}_{1}^{2}}$=1$<\frac{5}{3}$.当n≥2时,bn=$\frac{1}{{a}_{n}^{2}}$=$\frac{1}{{n}^{2}}$<$\frac{1}{{n}^{2}-\frac{1}{4}}$=$\frac{4}{4{n}^{2}-1}$=2$(\frac{1}{2n-1}-\frac{1}{2n+1})$.即可证明.
解答 (1)解:∵a${\;}_{n}^{2}+{a}_{n}$=2Sn,∴当n=1时,${a}_{1}^{2}+{a}_{1}=2{a}_{1}$,又a1>0,解得a1=1.
又${a}_{n+1}^{2}+{a}_{n+1}=2{S}_{n+1}$,∴${a}_{n+1}^{2}+{a}_{n+1}$-(a${\;}_{n}^{2}+{a}_{n}$)=2an+1,
化为(an+1+an)(an+1-an-1)=0,
∵?∈N*,an>0,可得an+1-an=1.
∴数列{an}是等差数列,首项为1,公差为1,an=1+(n-1)=n.
(2)证明:n=1时,b1=$\frac{1}{{a}_{1}^{2}}$=1$<\frac{5}{3}$.当n≥2时,bn=$\frac{1}{{a}_{n}^{2}}$=$\frac{1}{{n}^{2}}$<$\frac{1}{{n}^{2}-\frac{1}{4}}$=$\frac{4}{4{n}^{2}-1}$=2$(\frac{1}{2n-1}-\frac{1}{2n+1})$.
∴Tn=b1+b2+…+bn<1+2$[(\frac{1}{3}-\frac{1}{5})$+$(\frac{1}{5}-\frac{1}{7})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$=1+2$(\frac{1}{3}-\frac{1}{2n+1})$<$\frac{5}{3}$-$\frac{2}{2n+1}$.
∴Tn$<\frac{5}{3}$.
点评 本题考查了递推关系的应用、等差数列的通项公式、“放缩法”、“裂项求和”,考查了推理能力与计算能力,属于中档题.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案| A. | -7 | B. | 2 | C. | -1 | D. | 5 |
| A. | b>a>c | B. | a>c>b | C. | c>a>b | D. | a>b>c |
| A. | (-∞,2] | B. | (-∞,4] | C. | (-∞,8] | D. | [-2,4] |
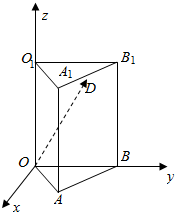 如图,在底面是边长为4的等边三角形的直三棱柱ABO-A1B1O1中,|AA1|=6,D为A1B1的中点,
如图,在底面是边长为4的等边三角形的直三棱柱ABO-A1B1O1中,|AA1|=6,D为A1B1的中点,