题目内容
3.已知:数列{an},{bn}满足$\left\{\begin{array}{l}{{a}_{n}{=\frac{2}{3}a}_{n-1}{+\frac{1}{3}b}_{n-1}}\\{{b}_{n}{=\frac{1}{3}a}_{n-1}{+\frac{2}{3}b}_{n-1}}\end{array}\right.$ (n≥2)且a1=10,b1=8,求an,bn的通项公式.分析 数列{an},{bn}满足$\left\{\begin{array}{l}{{a}_{n}{=\frac{2}{3}a}_{n-1}{+\frac{1}{3}b}_{n-1}}\\{{b}_{n}{=\frac{1}{3}a}_{n-1}{+\frac{2}{3}b}_{n-1}}\end{array}\right.$ (n≥2)且a1=10,b1=8,可得a2,b2,a3,b3.变形an-2bn=$\frac{1}{3}{b}_{n-1}-\frac{4}{3}{b}_{n-1}$,可得an=2bn+bn-1,
当n≥3时,an-1=2bn-1-bn-2.代入化为bn-bn-1=$\frac{1}{3}({b}_{n-1}-{b}_{n-2})$,利用等比数列的通项公式可得bn+1-bn=2×$\frac{1}{{3}^{n}}$.再利用bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1,同理可得an.
解答 解:∵数列{an},{bn}满足$\left\{\begin{array}{l}{{a}_{n}{=\frac{2}{3}a}_{n-1}{+\frac{1}{3}b}_{n-1}}\\{{b}_{n}{=\frac{1}{3}a}_{n-1}{+\frac{2}{3}b}_{n-1}}\end{array}\right.$ (n≥2)且a1=10,b1=8,
∴a2=$\frac{28}{3}$,b2=$\frac{26}{3}$,a3=$\frac{82}{9}$,b3=$\frac{80}{9}$.
an-2bn=$\frac{1}{3}{b}_{n-1}-\frac{4}{3}{b}_{n-1}$,可得an=2bn+$\frac{1}{3}{b}_{n-1}-\frac{4}{3}{b}_{n-1}$,
当n≥3时,an-1=2bn-1-bn-2.
∴bn=$\frac{1}{3}(2{b}_{n-1}-{b}_{n-2})$+$\frac{2}{3}{b}_{n-1}$,
化为bn-bn-1=$\frac{1}{3}({b}_{n-1}-{b}_{n-2})$,
∴数列{bn-bn-1}(n≥2)是等比数列,
首项为$\frac{2}{3}$,公比为$\frac{1}{3}$,
∴bn+1-bn=$\frac{2}{3}×(\frac{1}{3})^{n-1}$=2×$\frac{1}{{3}^{n}}$.
∴bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=2$(\frac{1}{{3}^{n-1}}+\frac{1}{{3}^{n-2}}+…+\frac{1}{3})$+8
=$2×\frac{\frac{1}{3}(1-\frac{1}{{3}^{n-1}})}{1-\frac{1}{3}}$+8=9-$\frac{1}{{3}^{n-1}}$.
当n≥2时,可得an=2bn-bn-1=$2(9-\frac{1}{{3}^{n-1}})$-$(9-\frac{1}{{3}^{n-2}})$=9+$\frac{1}{{3}^{n-1}}$.
当n=1时,上式也成立,∴an=9+$\frac{1}{{3}^{n-1}}$.
点评 本题考查了递推关系、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
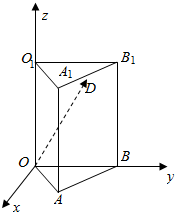 如图,在底面是边长为4的等边三角形的直三棱柱ABO-A1B1O1中,|AA1|=6,D为A1B1的中点,
如图,在底面是边长为4的等边三角形的直三棱柱ABO-A1B1O1中,|AA1|=6,D为A1B1的中点,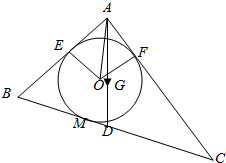 △ABC中,$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}$=$\overrightarrow{0}$O为△ABC内切圆的圆心,且AB=2,AC=3,BC=4.
△ABC中,$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}$=$\overrightarrow{0}$O为△ABC内切圆的圆心,且AB=2,AC=3,BC=4.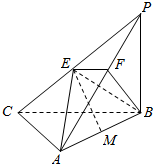 在三棱锥P-ABC中,PB⊥地面ABC,∠BCA=90°,E,M分别为PC,AB的中点,点F在PA上,且AF=2FP.
在三棱锥P-ABC中,PB⊥地面ABC,∠BCA=90°,E,M分别为PC,AB的中点,点F在PA上,且AF=2FP.