题目内容
5.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为单位向量,其中$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=$\overrightarrow{{e}_{2}}$,且$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为2,则$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 由$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为2,得$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{(2\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}})•\overrightarrow{{e}_{2}}}{|\overrightarrow{{e}_{2}}|}$=$\frac{2\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+|\overrightarrow{{e}_{2}}{|}^{2}}{1}=2|\overrightarrow{{e}_{1}}|•|\overrightarrow{{e}_{2}}|cos<\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}>$+1=2,得出cos<$\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}$>=$\frac{1}{2}$,则答案可求.
解答 解:由题意可得:
$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{(2\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}})•\overrightarrow{{e}_{2}}}{|\overrightarrow{{e}_{2}}|}$=$\frac{2\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+|\overrightarrow{{e}_{2}}{|}^{2}}{1}=2|\overrightarrow{{e}_{1}}|•|\overrightarrow{{e}_{2}}|cos<\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}>$+1=2,
解得cos$<\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}>$=$\frac{1}{2}$,
∵$<\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}>$∈[0,π],
∴$<\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}>$=$\frac{π}{3}$,
故选:C.
点评 本题考查向量的基本运算,考查单位向量、向量的投影等概念,解题的关键是对向量投影的理解,是中档题.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案(Ⅰ) 若c=2a,求角A、B、C的大小;
(Ⅱ) 当△ABC为锐角三角形时,求sinA+sinB+sinC的取值范围.
| A. | a≥4或a≤-2 | B. | a≥2或a≤-4 | C. | -2<a<4 | D. | -4<a<2 |
表1:男生
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
( II)由表中统计数据填写下面2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”?
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
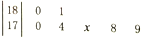 一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图如图所示,已知记录的平均身高为177cm,有1名选手的身高记录不清楚,其末位数记为x,那么x的值为( )
一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图如图所示,已知记录的平均身高为177cm,有1名选手的身高记录不清楚,其末位数记为x,那么x的值为( )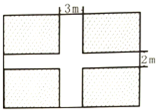 某校计划新建一个占地面积为600m2的停放自行车的矩形场地,在矩形场地中间保留宽分别为2m和3m的十字型通道,如图所示,当矩形用地的边长各为多少时,自行车停放地(阴影部分)的占地面积最大?最大面积是多少?
某校计划新建一个占地面积为600m2的停放自行车的矩形场地,在矩形场地中间保留宽分别为2m和3m的十字型通道,如图所示,当矩形用地的边长各为多少时,自行车停放地(阴影部分)的占地面积最大?最大面积是多少?