题目内容
15.为了判断高二学生选择文理是否与性别有关,现随机抽取50名学生,得到如下2×2列联表若p(k2≥3.841)≈0.05,p(k2≥5.024)≈0.025根据计算公式k2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$≈4.844则认为选修文理科与性别有关系出错的可能性为0.05.| 理科 | 文科 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
分析 根据条件中所给的观测值,同所给的临界值进行比较,根据4.844>3.841,即可得到结论.
解答 解:由题意,根据表中数据,得到k2=4.844>3.841,
由于P(x2≥3.841)≈0.05,
∴认为选修文理科与性别有关系出错的可能性为0.05.
故答案为:0.05.
点评 本题考查独立性检验的应用,解题的关键是正确理解观测值对应的概率的意义.

练习册系列答案
相关题目
5.已知$\frac{{2{{sin}^2}θ+sin2θ}}{1+tanθ}=k,0<θ<\frac{π}{4}$,则$sin(θ-\frac{π}{4})$的值( )
| A. | 随着k的增大而增大 | |
| B. | 有时随着k的增大而增大,有时随着k的增大而减小 | |
| C. | 随着k的增大而减小 | |
| D. | 是一个与k无关的常数 |
3.若函数f(x)(x∈R)对任意x1≠x2,都有x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1),则函数f(x)是( )
| A. | 增函数 | B. | 减函数 | C. | 奇函数 | D. | 偶函数 |
10.已知a为如图所示的算法框图中输出的结果,则a的值为( )
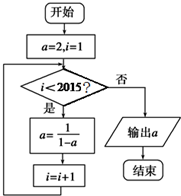

| A. | 2 | B. | -1 | C. | $\frac{1}{2}$ | D. | -2 |
20.过点(3,-2)且与椭圆4x2+9y2=36有相同焦点的椭圆的方程是( )
| A. | $\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{15}$=1 | B. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{10}$=1 | C. | $\frac{{x}^{2}}{15}$+$\frac{{y}^{2}}{10}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{10}$=1 |
5.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为单位向量,其中$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=$\overrightarrow{{e}_{2}}$,且$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为2,则$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
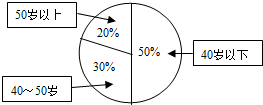 如图是某单位200名职工的年龄分布情况,现要从中抽取40名职工样本,用系统抽样法,将全体职工随机按1~200编号,并按
如图是某单位200名职工的年龄分布情况,现要从中抽取40名职工样本,用系统抽样法,将全体职工随机按1~200编号,并按