Question

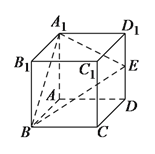
【题目】如图所示，在正方体中， 是棱的中点．

（）求直线和平面所成角的正弦值．

（）在棱上是否存在一点，使平面？证明你的结论．

Answer 1

【答案】（1）；（2）见解析.

【解析】试题分析：（1）先取AA1的中点M，连接EM，BM，根据中位线定理可知EM∥AD，而AD⊥平面ABB1A1，则EM⊥面ABB1A1，从而BM为直线BE在平面ABB1A1上的射影，则∠EBM直线BE与平面ABB1A1所成的角，设正方体的棱长为2，则EM=AD=2，BE=3，于是在Rt△BEM中，求出此角的正弦值即可．
（2）在棱C1D1上存在点F，使B1F平面A1BE，分别取C1D1和CD的中点F，G，连接EG，BG，CD1，FG，因A1D1∥B1C1∥BC，且A1D1=BC，所以四边形A1BCD1为平行四边形，根据中位线定理可知EG∥A1B，从而说明A1，B，G，E共面，则BG面A1BE，根据FG∥C1C∥B1G，且FG=C1C=B1B，从而得到四边形B1BGF为平行四边形，则B1F∥BG，而B1F平面A1BE，BG平面A1BE，根据线面平行的判定定理可知B1F∥平面A1BE．

试题解析：

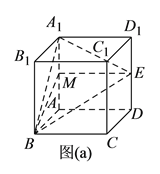
（）如图（a），取的中点，连接， ，因为是的中点，四边形为正方形，所以，

又在正方体中， 平面，所以面，从而为直线在平面上的射影，

直线与平面所成的角．设正方体的棱长为，则， ，

于是在中， ，

即：直线与平面所成的角的正弦值为．

（）在棱上存在点，使平面，

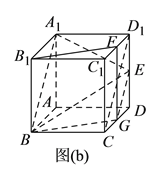
事实上，如图（b）所示，分别取和的中点、，连接、、、，

因，且，所以四边形为平行四边形，

因此，又， 分别为， 的中点，所以，从而，这说明， ， ， 共面，

所以平面，

因四边形与，皆为正方形， 分别为和的中点，

所以，且，

因此四边形为平行四边形，所以，而平面， 平面，

故平面．