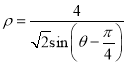题目内容
【题目】电视台播放甲、乙两套连续剧，每次播放连续剧时，需要播放广告．已知每次播放甲、乙两套连续剧时，连续剧播放时长、广告播放时长、收视人次如下表所示：
连续剧播放时长（分钟） | 广告播放时长（分钟） | 收视人次（万） | |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟，广告的总播放时间不少于30分钟，且甲连续剧播放的次数不多于乙连续剧播放次数的2倍．分别用
，
表示每周计划播出的甲、乙两套连续剧的次数．
（1）用，列出满足题目条件的数学关系式，并画出相应的平面区域；
（2）问电视台每周播出甲、乙两套连续剧各多少次，才能使收视人次最多？
【答案】（1）见解析；（2）每周播出甲连续剧6次、乙连续剧3次时才能使总收视人次最多．
【思路分析】（1）根据题目中的条件列出相应的不等式，同时注意
，
需满足
，
这一隐含条件，建立不等式组，画出平面区域；（2）根据
的几何意义即可求得最值．
【解析】（1）由已知，
满足的数学关系式为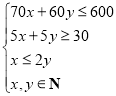
，即
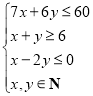．（2分）
该二元一次不等式组所表示的平面区域为图1中阴影部分内的整点（包括边界）：（5分）
（2）设总收视人次为
万，则目标函数为
．
考虑，将它变形为
，这是斜率为
，随变化的一族平行直线．
为直线在
轴上的截距，当取得最大值时，的值最大．（6分）
又
满足约束条件，所以由图2可知，当直线经过可行域上的点M时，截距最大，即最大．（8分）
解方程组
，得点M的坐标为
，
所以，电视台每周播出甲连续剧6次、乙连续剧3次时才能使总收视人次最多．（10分）
练习册系列答案
相关题目
