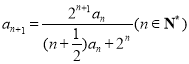题目内容
【题目】有两个分类变量x与y,其一组观测值如下面的2×2列联表所示:
y1 | y2 | |
x1 | a | 20-a |
x2 | 15-a | 30+a |
其中a,15-a均为大于5的整数,则a取何值时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系?
【答案】a为8或9时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系.
【解析】试题分析:这是一个独立性检验应用题,处理本题的关键根据列联表,及K2的计算公式,计算出K2的值,并代入临界值表中进行比较,列出一个关于a的不等式组,解不等式组后,再根据a的取值范围,即可得到答案.
试题解析:
查表可知,要使在犯错误的概率不超过0.1的前提下认为x与y之间有关系,则k≥2.706,而
k=![]()
=![]() =
=![]() .
.
由k≥2.706得a≥7.19或a≤2.04.
又a>5且15-a>5,a∈Z,
解得a=8或9.
故a为8或9时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系.

练习册系列答案
相关题目
【题目】一台机器由于使用时间较长,生产的零件有一些缺损.按不同转速生产出来的零件有缺损的统计数据如下表所示:
转速x(转/秒) | 16 | 4 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围内?