题目内容
11.设等差数列{an}的公差为d,点(an,bn)在f(x)=2x的图象上,若a1=-2,点(a8,4a7)在图象上,求an的前n项和.分析 通过将点(a8,4a7)代入f(x)=2x,化简可知a1+5d=0,利用a1=-2可知公差,进而可得结论.
解答 解:∵点(a8,4a7)在f(x)=2x的图象上,
∴2a8=4a7,即2(a1+7d)=4(a1+6d),
化简得:a1+5d=0,
又∵a1=-2,
∴d=-$\frac{{a}_{1}}{5}$=-$\frac{-2}{5}$=$\frac{2}{5}$,
∴Sn=na1+$\frac{n(n-1)}{2}$•d
=-2n+$\frac{2}{5}$•$\frac{n(n-1)}{2}$
=$\frac{1}{5}$n2-$\frac{11}{5}$n.
点评 本题考查数列的前n项和,考查运算求解能力,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
2.计算tan20°+$\frac{2sin40°}{cos20°}$的值为( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
16.抛掷一颗骰子得到的点数记为m,对于函数f(x)=sinπx,则“y=f(x)在[0,m]上至少有5个零点”的概率是( )
| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
20.若a>0,b>0,且a+b=4,则下列不等式恒成立的是( )
| A. | $\frac{1}{ab}>\frac{1}{2}$ | B. | a2+b2≥8 | C. | $\sqrt{ab}$≥2 | D. | $\frac{1}{a}+\frac{1}{b}$≤1 |
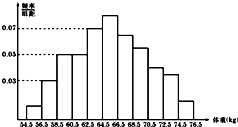 为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8.
为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8.