题目内容
已知函数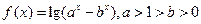
(1)求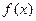 的定义域;
的定义域;
(2)在函数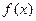 的图象上是否存在不同的两点,使过这两点的直线平行于
的图象上是否存在不同的两点,使过这两点的直线平行于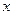 轴;
轴;
(3)当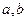 满足什么条件时,
满足什么条件时,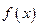 在
在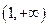 上恒取正值.
上恒取正值.
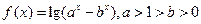
(1)求
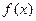 的定义域;
的定义域;(2)在函数
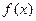 的图象上是否存在不同的两点,使过这两点的直线平行于
的图象上是否存在不同的两点,使过这两点的直线平行于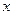 轴;
轴;(3)当
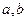 满足什么条件时,
满足什么条件时,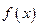 在
在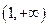 上恒取正值.
上恒取正值.(1) (2)不存在(3)
(2)不存在(3) 时,
时,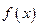 在
在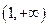 上恒取正值
上恒取正值
 (2)不存在(3)
(2)不存在(3) 时,
时,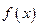 在
在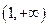 上恒取正值
上恒取正值解:(1) ,
,
又 ,故函数的定义域是
,故函数的定义域是
(2) 任取 ,则
,则 ,
,
 ,
,
 即
即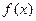 在定义域内单调递增
在定义域内单调递增
所以任取 则必有
则必有 故函函数
故函函数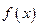 的图象L不存在不同的两点使过两点的直线平行于
的图象L不存在不同的两点使过两点的直线平行于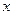 轴.
轴.
(3)因为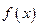 是增函数,所以当
是增函数,所以当 时,
时, ,
,
这样只需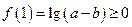 ,
,
即当 时,
时,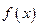 在
在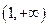 上恒取正值
上恒取正值
 ,
,又
 ,故函数的定义域是
,故函数的定义域是
(2) 任取
 ,则
,则 ,
, ,
, 即
即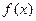 在定义域内单调递增
在定义域内单调递增所以任取
 则必有
则必有 故函函数
故函函数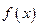 的图象L不存在不同的两点使过两点的直线平行于
的图象L不存在不同的两点使过两点的直线平行于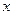 轴.
轴.(3)因为
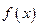 是增函数,所以当
是增函数,所以当 时,
时, ,
,这样只需
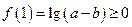 ,
,即当
 时,
时,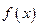 在
在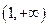 上恒取正值
上恒取正值
练习册系列答案
相关题目
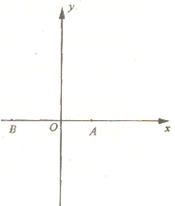
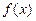 是定义在
是定义在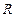 上的单调奇函数, 且
上的单调奇函数, 且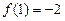 .
.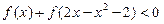 .
.
 和
和 的图象在
的图象在 处的切线互相平行.
处的切线互相平行. 的值;
的值; ,当
,当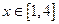 时,
时, 恒成立,求
恒成立,求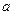 的取值范围.
的取值范围. ,若初时含杂质
,若初时含杂质 ,每过滤一次可使杂质含量减少
,每过滤一次可使杂质含量减少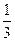 ,问至少应过滤几次才能使产品达到市场要求?(已知
,问至少应过滤几次才能使产品达到市场要求?(已知 )
)
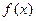 是奇函数,
是奇函数,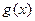 是偶函数,并且
是偶函数,并且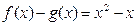 ,求
,求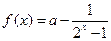 ,(
,(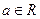 )
)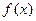 的定义域;
的定义域;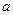 的值;
的值;