题目内容
已知定点A(a,O)( a >0),B为x轴负半轴上的动点.以AB为边作菱形ABCD,使其两对角线的交点恰好落在y轴上.
(I)求动点D的轨迹E的方程;
(Ⅱ)过点A作直线l与轨迹E交于P、Q两点,设点R (- a,0),问当l绕点A转动时,∠PRQ是否可以为钝角?请给出结论,并加以证明.
(I)求动点D的轨迹E的方程;

(Ⅱ)过点A作直线l与轨迹E交于P、Q两点,设点R (- a,0),问当l绕点A转动时,∠PRQ是否可以为钝角?请给出结论,并加以证明.
详见解析
解法一:(Ⅰ)设D(x,y),∵A(a,0),由ABCD为菱形
 且AC、BD的交点在y轴上,
且AC、BD的交点在y轴上,
∴B、C两点坐标为(-x,0)、(-a,y).
由AC⊥BD得
 ·
·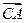 =(2x,y)·(2a,-y)
=(2x,y)·(2a,-y)
=4ax - y2=0,
即 y2 = 4ax.
注意到ABCD为菱形,∴x≠0
故轨迹E的方程为y2 = 4ax(x≠0).
(Ⅱ)∠PRQ不可能为钝角,即∠PRQ≤90°.
证明如下:
(1)当PQ⊥x轴时,P、Q点的坐标为(a,±2a),又R(一a,0),
此时∠PRQ=90°,结论成立;
(2)当PQ与x轴不垂直时,设直线PQ的方程为y=k(x一a),
由 得 k2x2 - (2ak2+4a)x + k2a2 = 0
得 k2x2 - (2ak2+4a)x + k2a2 = 0
记P(x1,y1),Q(x2,y2),则x1+x2=2a+ ,x1 x2=a2.
,x1 x2=a2.
 ·
·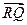 =(x1+a)(x2+a)+y1y2
=(x1+a)(x2+a)+y1y2
=(x1+a)(x2+a)+k2(x1- a)(x2- a)
=(1+k2) x1 x2+(a - ak2)( x1+x2)+a2+a2k2
=(1+k2) a2 +(a - ak2)( 2a+ )+a2+a2k2=
)+a2+a2k2= >0
>0
即< ,
,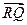 >为锐角,
>为锐角,
综上(1)、(2)知∠PRQ≤90°成立.
解法二:(Ⅰ)设D(x,y),由ABCD为菱形且AC、BD的交点在y轴上,
∴C点坐标为(-a,y),∵A(a,0),由|DA|=|DC|得
 ,
,
化简得y2=4ax.
注意到ABCD为菱形,∴x≠O,
故轨迹E的方程为y2=4ax(x≠O).
(Ⅱ)∠PRQ不可能为钝角,即∠PRQ≤90°
证明如下:
设P(x1,y1),Q(x2,y2),同证法一易知,则x1 x2=a2.又y12=4ax1,y22=4ax2,且|PR|2=x1+x2+2a ,因为
|PR|2+|QR|2-|PQ|2=(x1+a)2+y12+(x2+a)2+y22-( x1+x2+2a)2
=2ax1+2ax2-4a2≥2 -4a2=4a
-4a2=4a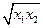 -4a2=0
-4a2=0
从而 cos∠PRQ=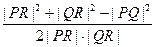 ≥0,
≥0,
即∠PRQ≤90°
解法三:(Ⅰ)因为ABCD为菱形,且AC与BD的交点在y轴上,
所以点C的横坐标为 -a,
即点C在直线x = -a上,从而D到C的距离等于D到直线x = -a的距 离.又ABCD为菱形,所以点D到点A的距离与点D到直线x = -a的距离 相等,即轨迹E为抛物线,方程为y2=4ax.
注意到ABCD为菱形,∴x≠O,
故轨迹E的方程为y2=4ax(x≠O).
(Ⅱ) ∠PRQ不可能为钝角,即∠PRQ≤90°
证明如下:
如图,过P、Q向x轴及准线x = -a引垂线,记垂足为M、N、C、H,
则|MR|=|PG|=|PA|≥|PM|,所以∠PRM≤45°,
同理可证∠QRN≤45°,从而∠PRQ≤90°
解法四:(Ⅰ)同解法一.
(Ⅱ) ∠PRQ不可能为钝角,即∠PRQ≤90°
证明如下:
设P(x1,y1),则y12=4ax1,tan∠PRM=|kPR|=|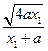 |=
|=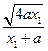 ,
,
∵x1+a≥2 ,∴tan∠PRA≤1,∠QRA≤45°,
,∴tan∠PRA≤1,∠QRA≤45°,
同理可证∠QRA≤45°,即∠PRQ≤90°
 且AC、BD的交点在y轴上,
且AC、BD的交点在y轴上,∴B、C两点坐标为(-x,0)、(-a,y).
由AC⊥BD得
 ·
·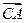 =(2x,y)·(2a,-y)
=(2x,y)·(2a,-y)=4ax - y2=0,
即 y2 = 4ax.
注意到ABCD为菱形,∴x≠0
故轨迹E的方程为y2 = 4ax(x≠0).
(Ⅱ)∠PRQ不可能为钝角,即∠PRQ≤90°.
证明如下:
(1)当PQ⊥x轴时,P、Q点的坐标为(a,±2a),又R(一a,0),
此时∠PRQ=90°,结论成立;
(2)当PQ与x轴不垂直时,设直线PQ的方程为y=k(x一a),
由
 得 k2x2 - (2ak2+4a)x + k2a2 = 0
得 k2x2 - (2ak2+4a)x + k2a2 = 0记P(x1,y1),Q(x2,y2),则x1+x2=2a+
 ,x1 x2=a2.
,x1 x2=a2. ·
·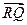 =(x1+a)(x2+a)+y1y2
=(x1+a)(x2+a)+y1y2=(x1+a)(x2+a)+k2(x1- a)(x2- a)
=(1+k2) x1 x2+(a - ak2)( x1+x2)+a2+a2k2
=(1+k2) a2 +(a - ak2)( 2a+
 )+a2+a2k2=
)+a2+a2k2= >0
>0即<
 ,
,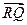 >为锐角,
>为锐角,综上(1)、(2)知∠PRQ≤90°成立.
解法二:(Ⅰ)设D(x,y),由ABCD为菱形且AC、BD的交点在y轴上,
∴C点坐标为(-a,y),∵A(a,0),由|DA|=|DC|得
 ,
,化简得y2=4ax.
注意到ABCD为菱形,∴x≠O,
故轨迹E的方程为y2=4ax(x≠O).
(Ⅱ)∠PRQ不可能为钝角,即∠PRQ≤90°
证明如下:
设P(x1,y1),Q(x2,y2),同证法一易知,则x1 x2=a2.又y12=4ax1,y22=4ax2,且|PR|2=x1+x2+2a ,因为
|PR|2+|QR|2-|PQ|2=(x1+a)2+y12+(x2+a)2+y22-( x1+x2+2a)2
=2ax1+2ax2-4a2≥2
 -4a2=4a
-4a2=4a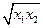 -4a2=0
-4a2=0从而 cos∠PRQ=
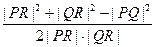 ≥0,
≥0,即∠PRQ≤90°
解法三:(Ⅰ)因为ABCD为菱形,且AC与BD的交点在y轴上,
所以点C的横坐标为 -a,
即点C在直线x = -a上,从而D到C的距离等于D到直线x = -a的距 离.又ABCD为菱形,所以点D到点A的距离与点D到直线x = -a的距离 相等,即轨迹E为抛物线,方程为y2=4ax.
注意到ABCD为菱形,∴x≠O,
故轨迹E的方程为y2=4ax(x≠O).
(Ⅱ) ∠PRQ不可能为钝角,即∠PRQ≤90°
证明如下:
如图,过P、Q向x轴及准线x = -a引垂线,记垂足为M、N、C、H,
则|MR|=|PG|=|PA|≥|PM|,所以∠PRM≤45°,
同理可证∠QRN≤45°,从而∠PRQ≤90°
解法四:(Ⅰ)同解法一.
(Ⅱ) ∠PRQ不可能为钝角,即∠PRQ≤90°
证明如下:
设P(x1,y1),则y12=4ax1,tan∠PRM=|kPR|=|
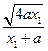 |=
|=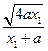 ,
,∵x1+a≥2
 ,∴tan∠PRA≤1,∠QRA≤45°,
,∴tan∠PRA≤1,∠QRA≤45°,同理可证∠QRA≤45°,即∠PRQ≤90°

练习册系列答案
相关题目
 为偶函数且在区间
为偶函数且在区间 上是单调增函数.
上是单调增函数. 的解析式;
的解析式; ,若
,若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.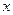 (百台),其总成本为
(百台),其总成本为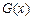 (万元),其中固定成本2万元,每生产1百台需生产成本1万元(总成本
(万元),其中固定成本2万元,每生产1百台需生产成本1万元(总成本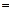 固定成本
固定成本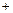 生产成本);销售收入
生产成本);销售收入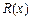 (万元)满足:
(万元)满足: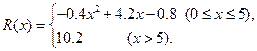 (Ⅰ)要使工厂有盈利,求
(Ⅰ)要使工厂有盈利,求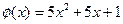
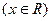 ,函数
,函数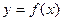 的图象与
的图象与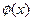 的图象关于点
的图象关于点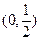 中心对称。
中心对称。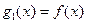 ,
,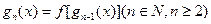 ,试求出使
,试求出使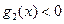 成立的
成立的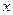 取值范围;
取值范围; ,使
,使 对于区间内的任意实数
对于区间内的任意实数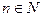 ,且
,且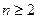 时,都有
时,都有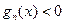 恒成立?
恒成立?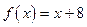 ,
,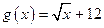 ,及任意的
,及任意的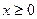 ,当甲公司投入
,当甲公司投入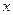 万元作宣传时,乙公司投入的宣传费若小于
万元作宣传时,乙公司投入的宣传费若小于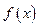 万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入
万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入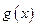 万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题:
万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题: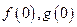 ;
;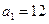 万元,乙在上述策略下,投入最少费用
万元,乙在上述策略下,投入最少费用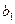 ;而甲根据乙的情况,调整宣传费为
;而甲根据乙的情况,调整宣传费为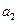 ;同样,乙再根据甲的情况,调整宣传费为
;同样,乙再根据甲的情况,调整宣传费为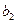
 如此得当甲调整宣传费为
如此得当甲调整宣传费为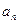 时,乙调整宣传费为
时,乙调整宣传费为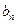 ;试问是否存在
;试问是否存在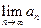 ,
,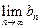 的值,若存在写出此极限值(不必证明),若不存在,说明理由.
的值,若存在写出此极限值(不必证明),若不存在,说明理由. 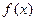 是一次函数,且
是一次函数,且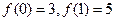 .
.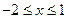 时,函数
时,函数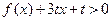 恒成立,求实数
恒成立,求实数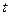 的取值范围
的取值范围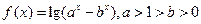
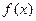 的定义域;
的定义域;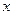 轴;
轴;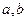 满足什么条件时,
满足什么条件时,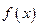 在
在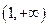 上恒取正值.
上恒取正值.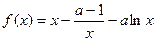
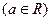 。
。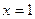 是函数
是函数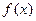 的极大值点,求
的极大值点,求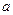 的取值范围;
的取值范围;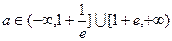 时,若在
时,若在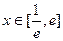 上至少存在一点
上至少存在一点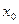 ,使
,使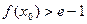 成立,求
成立,求