题目内容
【题目】如图，游客从景点
下山至
有两种路径：一种是从沿直线步行到，另一种是先从乘缆车到
，然后从沿直线步行到.现有甲、乙两位游客从下山，甲沿
匀速步行，速度为
米/分钟.在甲出发
分钟后，乙从乘缆车到，在处停留
分钟后，再从匀速步行到.已知缆车从到要
分钟， 长为
米，若
，
.为使两位游客在处互相等待的时间不超过
分钟，则乙步行的速度
（米/分钟）的取值范围是 __________．
【答案】
【解析】分析：由题意结合正弦定理余弦定理首先解三角形，然后结合实际问题得到关于速度的不等式，求解不等式即可求得最终结果.
详解：在△ABC中解三角形：
已知
，
，
，则：
，
由正弦定理可得：
，
由余弦定理
有：
，
解得：
，
若
，则
，不能组成三角形，舍去，
据此可得：
.
乙从B出发时,甲已经走了50×(2+8+1)=550m，还需走710m才能到达C.
设乙步行的速度为vm/min,由题意得
,解得
,
所以为使两位游客在C处互相等待的时间不超过3分钟,
乙步行的速度应控制在范围内.
【题目】目前，学案导学模式已经成为教学中不可或缺的一部分，为了了解学案的合理使用是否对学生的期末复习有着重要的影响某校随机抽取200名学生，对学习成绩和学案使用程度进行了调查，统计数据如下表所示：
善于使用学案 | 不善于使用学案 | 合计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
合计 | 200 |
已知随机抽查这200名学生中的一名学生，抽到善于使用学案的学生概率是0.6.
参考公式：
，其中
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
（I）完成
列联表（不用写计算过程）；
（Ⅱ）试运用独立性检验的思想方法分析有多大的把握认为学生的学习成绩与对待学案的使用态度有关？
【题目】某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
【题目】从某小区抽取50户居民进行月用电量调查，发现其用电量都在50到350度之间，将用电量的数据绘制成频率分布直方图如下.
（1）求频率分布直方图中
的值并估计这50户用户的平均用电量；
（2）若将用电量在区间
内的用户记为
类用户，标记为低用电家庭，用电量在区间
内的用户记为
类用户，标记为高用电家庭，现对这两类用户进行问卷调查，让其对供电服务进行打分，打分情况见茎叶图：
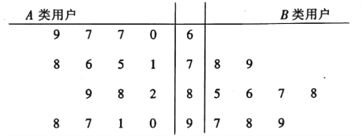
①从
类用户中任意抽取3户，求恰好有2户打分超过85分的概率；
②若打分超过85分视为满意，没超过85分视为不满意，请填写下面列联表，并根据列联表判断是否有
的把握认为“满意度与用电量高低有关”？
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
， 
.
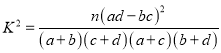