题目内容
9.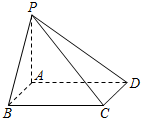 如图,在四棱锥P-ABCD中,底面正方形ABCD为边长为2,PA⊥底面ABCD,E为BC的中点,PC与平面PAD所成的角为arctan$\frac{{\sqrt{2}}}{2}$.
如图,在四棱锥P-ABCD中,底面正方形ABCD为边长为2,PA⊥底面ABCD,E为BC的中点,PC与平面PAD所成的角为arctan$\frac{{\sqrt{2}}}{2}$.(1)求异面直线AE与PD所成角的大小(结果用反三角函数表示);
(2)求点B到平面PCD的距离.
分析 (1)根据PC与平面PAD所成的角求出PD的大小,进而求PA的大小,从而建立空间直角坐标系,解答即可;
(2)利用等积法求点到面的距离即可.
解答 解:∵PA⊥底面ABCD,CD?面ABCD,
∴CD⊥PA,
又在正方形ABCD中,CD⊥AD,
∴CD⊥平面PAD,
∴PC与平面PAD所成的角为∠CPD,
故tan∠CPD=$\frac{CD}{PD}$=$\frac{\sqrt{2}}{2}$,
又CD=2,
∴PD=2$\sqrt{2}$,
PA2+AD2=PD2,
∴PA=2,
以A为原点,分别以AB,AD,AP为x,y,z轴建立空间直角坐标系,则: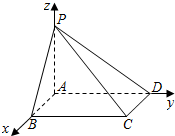
A(0,0,0),E(2,1,0),P(0,0,2),D(0,2,0)
∴$\overrightarrow{AE}$=(2,1,0),$\overrightarrow{PD}=(0,2,-2)$,
∴cos<$\overrightarrow{AE},\overrightarrow{PD}$>=$\frac{\overrightarrow{AE}•\overrightarrow{PD}}{|\overrightarrow{AE}|•|\overrightarrow{PD}|}$=$\frac{\sqrt{10}}{10}$,
所以异面直线AE与PD所成角的大小为arccos$\frac{\sqrt{10}}{10}$;
(2)∵VB-PCD=VP-BCD,设B到平面PCD的距离为d,则有:
$\frac{1}{3}d{S}_{△PCD}=\frac{1}{3}PA•{S}_{△BCD}$,
即:$\frac{1}{3}d•\frac{1}{2}×2×2\sqrt{2}$=$\frac{1}{3}×2×\frac{1}{2}×2×2$,
解得d=$\sqrt{2}$,
所以点B到平面PCD的距离为$\sqrt{2}$.
点评 本题主要考查线与面的夹角、直线与直线的夹角以及等积法,属于中档题.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案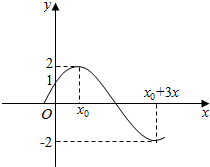 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图 