题目内容
18.将(x+y+z+k)12展开式为多项式,经合并后共有多少个不同的项?分析 利用组合模型求解该问题,恰当构造分组模型,利用组合法解决该问题.
解答 解:对于这个式子,可以知道必定会有形如qxaybzckd的式子出现,其中q∈R,a,b,c,d∈N
而且a+b+c+d=12,
构造16个完全一样的小球模型,分成3组,每组至少一个,共有分法${C}_{15}^{3}$种,
每一组中都去掉一个小球的数目分别作为(x+y+z+k)12的展开式中每一项中x,y,z,k各字母的次数.
小球分组模型与各项的次数是一一对应的.
故(x+y+z+k)12的展开式中,合并同类项之后的项数为${C}_{15}^{3}$.
点评 本题主要考查了二项展开式的系数特征,考查构造法解决该问题,关键要构造一个适当的组合模型,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
16.函数y=f(x)的图象如图,则f(x)的定义域是( )
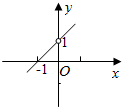
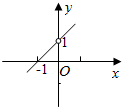
| A. | R | B. | (-∞,1)∪(1,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-1,0) |
7.在约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{y+x≤4}\\{y+2x≤s}\end{array}\right.$下,当2≤s≤8时,目标函数z=3x+2y的最大值的变化范围是( )
| A. | [3,12] | B. | [4,12] | C. | [3,8] | D. | [6,12] |
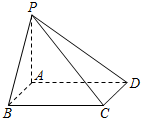 如图,在四棱锥P-ABCD中,底面正方形ABCD为边长为2,PA⊥底面ABCD,E为BC的中点,PC与平面PAD所成的角为arctan$\frac{{\sqrt{2}}}{2}$.
如图,在四棱锥P-ABCD中,底面正方形ABCD为边长为2,PA⊥底面ABCD,E为BC的中点,PC与平面PAD所成的角为arctan$\frac{{\sqrt{2}}}{2}$.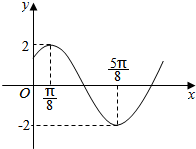 已知函数y=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示:
已知函数y=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示: