题目内容
7.若f(x)对定义域(0,+∞)内任意x,y都有f($\frac{x}{y}$)=f(x)-f(y),且f(2)=1,则f($\frac{\sqrt{2}}{2}$)=-$\frac{1}{2}$.分析 由条件,可令x=2,y=$\sqrt{2}$可得f($\sqrt{2}$),再令x=$\sqrt{2}$,y=2可得f($\frac{\sqrt{2}}{2}$).
解答 解:由f($\frac{x}{y}$)=f(x)-f(y),
令x=2,y=$\sqrt{2}$可得f($\frac{2}{\sqrt{2}}$)=f(2)-f($\sqrt{2}$),
由f(2)=1,可得f($\sqrt{2}$)=$\frac{1}{2}$,
再令x=$\sqrt{2}$,y=2可得f($\frac{\sqrt{2}}{2}$)=f($\sqrt{2}$)-f(2)=$\frac{1}{2}$-1
=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查抽象函数的应用,考查赋值法的运用,正确赋值是解题的关键.

练习册系列答案
相关题目
16.函数y=f(x)的图象如图,则f(x)的定义域是( )
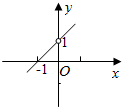
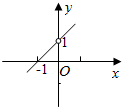
| A. | R | B. | (-∞,1)∪(1,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-1,0) |
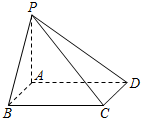 如图,在四棱锥P-ABCD中,底面正方形ABCD为边长为2,PA⊥底面ABCD,E为BC的中点,PC与平面PAD所成的角为arctan$\frac{{\sqrt{2}}}{2}$.
如图,在四棱锥P-ABCD中,底面正方形ABCD为边长为2,PA⊥底面ABCD,E为BC的中点,PC与平面PAD所成的角为arctan$\frac{{\sqrt{2}}}{2}$.