Question

【题目】设等差数列{an}的公差d＞0，且a1＞0，记Tn= + ++ ．
（1）用a1、d分别表示T1、T2、T3 ， 并猜想Tn；
（2）用数学归纳法证明你的猜想．

Answer 1

【答案】
（1）解：T1= = ；

T2= + = （ ）+ （ ﹣ ）= （ ）= = ；

T3= + + = （ ）+ （ ﹣ ）+ （ ﹣ ）= （ ﹣ ）= = ；

由此可猜想Tn= ．

（2）证明：①当n=1时，T1= ，结论成立，

②假设当n=k时（k∈N*）时结论成立，

即Tk= ，

则当n=k+1时，Tk+1=Tk+ = + =

= = ．

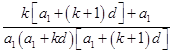
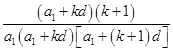即n=k+1时，结论成立．

由①②可知，Tn= 对于一切n∈N*恒成立．

【解析】（1）利用裂项法计算T1、T2、T3，并猜想结论；（2）先验证n=1，再假设n=k猜想成立，推导n=k+1猜想成立．
【考点精析】认真审题，首先需要了解归纳推理(根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理)．