题目内容
【题目】求分别满足下列条件的直线l的方程:
(1)斜率是![]() ,且与两坐标轴围成的三角形的面积是6;
,且与两坐标轴围成的三角形的面积是6;
(2)经过两点A(1,0)、B(m,1);
(3)经过点(4,-3),且在两坐标轴上的截距的绝对值相等.
【答案】(1)y=![]() x±3.(2)当m≠1时,y=
x±3.(2)当m≠1时,y=![]() (x-1),当m=1时, x=1.(3)x+y=1或
(x-1),当m=1时, x=1.(3)x+y=1或![]() 或y=-
或y=-![]() x.
x.
【解析】试题分析:(1)利用斜截式设出直线方程,得到直线的截距,表示三角形的面积,从而得到直线l的方程;(2)分三种情况讨论,过原点,不过原点斜率为1,不过原点斜率为-1,从而得到直线的方程
试题解析:
(1)设直线l的方程为y=![]() x+b.
x+b.
令y=0,得x=-![]() b,
b,
∴![]() |b·(-
|b·(-![]() b)|=6,b=±3.
b)|=6,b=±3.
∴直线l的方程为y=![]() x±3.
x±3.
(2)当m≠1时,直线l的方程是
![]() =
=![]() ,即y=
,即y=![]() (x-1)
(x-1)
当m=1时,直线l的方程是x=1.
(3)设l在x轴、y轴上的截距分别为a、b.
当a≠0,b≠0时,l的方程为![]() +
+![]() =1;
=1;
∵直线过P(4,-3),∴![]() -
-![]() =1.
=1.
又∵|a|=|b|,
∴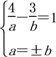 ,解得
,解得![]() ,或
,或![]() .
.
当a=b=0时,直线过原点且过(4,-3),
∴l的方程为y=-![]() x.
x.
综上所述,直线l的方程为x+y=1或![]() +
+![]() =1或y=-
=1或y=-![]() x.
x.

练习册系列答案
相关题目
【题目】某高中为了解高中学生的性别和喜欢打篮球是否有关,对50名高中学生进行了问卷调查,得到如下列联表:
喜欢打篮球 | 不喜欢打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
已知在这50人中随机抽取1人,抽到喜欢打篮球的学生的概率为 ![]()
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.5%的把握认为喜欢打篮球与性别有关?
附:K2= ![]()
p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |