函数y=$\sqrt{x}$-$\sqrt{4-x}$的值域是( )A．[2.2$\sqrt{2}$]B．[4.8]C．[-2.2]D．[0.2$\sqrt{2}$] 题目和参考答案——青夏教育精英家教网——

题目内容

13．函数y=$\sqrt{x}$-$\sqrt{4-x}$的值域是（　　）

A．

[2，2$\sqrt{2}$]

B．

[4，8]

C．

[-2，2]

D．

[0，2$\sqrt{2}$]

分析根据题意，先求出函数的定义域，进而分析可得函数y=$\sqrt{x}$-$\sqrt{4-x}$在其定义域上是增函数，结合函数的定义域，可得答案．

解答解：由题意易知，$\left\{\begin{array}{l}{x≥0}\\{4-x≥0}\end{array}\right.$，
故函数的定义域为[0，4]；
易知函数y=$\sqrt{x}$-$\sqrt{4-x}$在[0，4]上是增函数，
故-2≤$\sqrt{x}$-$\sqrt{4-x}$≤2；
即函数y=$\sqrt{x}$+$\sqrt{4-x}$的值域是[-2，2]；
故选C．

点评本题考查函数的值域，涉及函数单调性的应用，关键是分析出函数的单调性．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

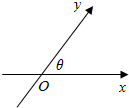如图，数轴x，y的交点为O，夹角为θ，与x轴、y轴正向同向的单位向量分别是$\overrightarrow{e_1}，\overrightarrow{e_2}$．由平面向量基本定理，对于平面内的任一向量$\overrightarrow{OP}$，存在唯一的有序实数对（x，y），使得$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$，我们把（x，y）叫做点P在斜坐标系xOy中的坐标（以下各点的坐标都指在斜坐标系xOy中的坐标）．
（1）若θ=90°，$\overrightarrow{OP}$为单位向量，且$\overrightarrow{OP}$与$\overrightarrow{e_1}$的夹角为120°，求点P的坐标；
（2）若θ=45°，点P的坐标为$（{1，\sqrt{2}}）$，求向量$\overrightarrow{OP}$与$\overrightarrow{e_1}$的夹角；
（3）若θ=60°，求过点A（2，1）的直线l的方程，使得原点O到直线l的距离最大．

4．数列{a_n}中，a_n≠0，a₁=2且2a_na_n-1+a_n-1-a_n=0（n∈N^*），则a₁₅=$-\frac{2}{55}$．

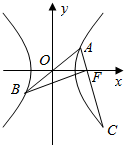如图所示，A，B，C是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）上的三个点，AB经过原点O，AC经过右焦点F，若BF⊥AC且|BF|=|CF|，则该双曲线的离心率是$\frac{{\sqrt{10}}}{2}$．

8．化简：${（{\frac{2}{3}}）^0}+{2^{-2}}×{（{\frac{9}{16}}）^{-\frac{1}{2}}}+（lg8+lg125）$=$\frac{13}{3}$．

18．已知点P为圆C：x²+y²-4x-4y+4=0上的动点，点P到某直线l的最大距离为5，若在直线l上任取一点A作圆C的切线AB，切点为B，则AB的最小值是$\sqrt{5}$．

5．已知函数f（x）=$\sqrt{2}sin（x+φ），0＜φ＜\frac{π}{2}$，且f（0）=1．
（1）求f（x）的解析式；
（2）已知$f（α-\frac{π}{4}）+f（α+\frac{π}{4}）=\frac{{4\sqrt{2}}}{5}$，且$\frac{3π}{2}$＜α＜2π，求sinα-cosα．

2．已知函数$f（x）=（{m^2}-m-1）{x^{{m^2}-2m-3}}$是幂函数，且f（x）在（0，+∞）上为减函数，${（a+1）^{\frac{1}{m}}}＜{（3-2a）^{\frac{1}{m}}}$，则实数a的取值范围为[-1，$\frac{2}{3}$）．

3．一个球内有一内接长方体，其长、宽、高分别为5，4，3，则球的半径为（　　）

$\frac{5\sqrt{2}}{2}$