题目内容
18.已知点P为圆C:x2+y2-4x-4y+4=0上的动点,点P到某直线l的最大距离为5,若在直线l上任取一点A作圆C的切线AB,切点为B,则AB的最小值是$\sqrt{5}$.分析 由题意可知圆心到直线l的距离为3,画出图形,由图可知满足题意的A点的位置,由勾股定理求得答案.
解答 解:由C:x2+y2-4x-4y+4=0,得(x-2)2+(y-2)2=4,
由圆上动点P到某直线l的最大距离为5,可知圆心(2,2)到直线l的最大距离为3,
如图,
若在直线l上任取一点A作圆C的切线AB,切点为B,则要使AB最小,需圆心C到直线l的距离最小,
∴AB的最小值是$\sqrt{A{C}^{2}-B{C}^{2}}=\sqrt{{3}^{2}-{2}^{2}}=\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查直线与圆的位置关系,考查了数形结合的数学思想方法,考查数学转化思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.下列命题中真命题是( )
| A. | 若$\overrightarrow{a}$与$\overrightarrow{b}$互为负向量,则$\overrightarrow{a}$+$\overrightarrow{b}$=0 | B. | 若 $\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$,则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C. | 若k为实数且k$\overrightarrow{a}$=$\overrightarrow{0}$,则k=0或$\overrightarrow{a}$=$\overrightarrow{0}$ | D. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为|$\overrightarrow{a}$| |
13.函数y=$\sqrt{x}$-$\sqrt{4-x}$的值域是( )
| A. | [2,2$\sqrt{2}$] | B. | [4,8] | C. | [-2,2] | D. | [0,2$\sqrt{2}$] |
7.三个数a=0.67,b=70.6,c=log0.76的大小关系为( )
| A. | b<c<a | B. | b<a<c | C. | c<a<b | D. | c<b<a |
8.要得到函数y=sin$\frac{1}{2}$x的图象,只需将函数y=sin($\frac{1}{2}$x+$\frac{π}{4}$)的图象( )
| A. | 向左平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{2}$个单位长度 |
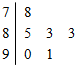 为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则该同学数学成绩的中位数为84.
为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则该同学数学成绩的中位数为84.