题目内容
1.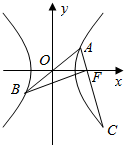 如图所示,A,B,C是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是$\frac{{\sqrt{10}}}{2}$.
如图所示,A,B,C是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是$\frac{{\sqrt{10}}}{2}$.
分析 运用直角三角形斜边上中线等于斜边的一半,求得A的坐标,由对称得B的坐标,由于BF⊥AC且|BF|=|CF|,
求得C的坐标,代入双曲线方程,结合a,b,c的关系和离心率公式,化简整理成离心率e的方程,代入选项即可得到答案.
解答 解:由题意可得在直角三角形ABF中,
OF为斜边AB上的中线,即有|AB|=2|OA|=2|OF|=2c,
设A(m,n),则m2+n2=c2,
又$\frac{{m}^{2}}{{a}^{2}}-\frac{{n}^{2}}{{b}^{2}}$=1,解得m=$\frac{a\sqrt{{c}^{2}+{b}^{2}}}{c}$,n=$\frac{{b}^{2}}{c}$,
即有A($\frac{a\sqrt{{c}^{2}+{b}^{2}}}{c}$,$\frac{{b}^{2}}{c}$),B(-$\frac{a\sqrt{{c}^{2}+{b}^{2}}}{c}$,-$\frac{{b}^{2}}{c}$),
又F(c,0),
由于BF⊥AC且|BF|=|CF|,
可设C(x,y),即有$\frac{y}{x-c}•\frac{{b}^{2}}{{c}^{2}+a\sqrt{{c}^{2}+{b}^{2}}}$=-1,
又(c+$\frac{a\sqrt{{c}^{2}+{b}^{2}}}{c}$)2+($\frac{{b}^{2}}{c}$)2=(x-c)2+y2,
可得x=$\frac{{b}^{2}+{c}^{2}}{c}$,y=-$\frac{a\sqrt{{c}^{2}+{b}^{2}}+{c}^{2}}{c}$,
将C($\frac{{b}^{2}+{c}^{2}}{c}$,-$\frac{a\sqrt{{c}^{2}+{b}^{2}}+{c}^{2}}{c}$)代入双曲线方程,化简可得$\sqrt{{c}^{2}+{b}^{2}}$(b2-a2)=a3,
由b2=c2-a2,e=$\frac{c}{a}$,得(2e2-1)(e2-2)2=1,
可得e=$\frac{{\sqrt{10}}}{2}$.
故答案为:$\frac{{\sqrt{10}}}{2}$.
点评 本题考查双曲线的方程和性质,主要考查双曲线的a,b,c的关系和离心率的求法,注意运用点在双曲线上满足方程,属于难题.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | 2π-9 | B. | 9-2π | C. | -1 | D. | 1 |
| A. | 若$\overrightarrow{a}$与$\overrightarrow{b}$互为负向量,则$\overrightarrow{a}$+$\overrightarrow{b}$=0 | B. | 若 $\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$,则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C. | 若k为实数且k$\overrightarrow{a}$=$\overrightarrow{0}$,则k=0或$\overrightarrow{a}$=$\overrightarrow{0}$ | D. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为|$\overrightarrow{a}$| |
| A. | [2,2$\sqrt{2}$] | B. | [4,8] | C. | [-2,2] | D. | [0,2$\sqrt{2}$] |