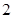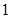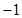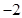题目内容
判断下列函数的奇偶性:
(1)f(x)=x3-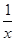 ;
;
(2)f(x)=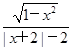 ;
;
(3)f(x)=(x-1)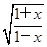 ;
;
(4)f(x)=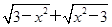 .
.
(1)f(x)=x3-
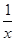 ;
;(2)f(x)=
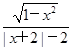 ;
;(3)f(x)=(x-1)
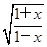 ;
;(4)f(x)=
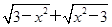 .
.(1)奇函数(2)奇函数(3)既不是奇函数也不是偶函数(4)既是奇函数也是偶函数
(1)定义域是(-∞,0)∪(0,+∞),关于原点对称,由f(-x)=-f(x),所以f(x)是奇函数.
(2)去掉绝对值符号,根据定义判断.由 得
得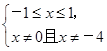 .
.
故f(x)的定义域为[-1,0)∪(0,1],关于原点对称,且有x+2>0.
从而有f(x)=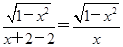 ,
,
这时有f(-x)= =-f(x),故f(x)为奇函数.
=-f(x),故f(x)为奇函数.
(3)因为f(x)定义域为[-1,1),所以f(x)既不是奇函数也不是偶函数.
(4)因为f(x)定义域为{-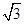 ,
,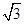 },所以f(x)=0,则f(x)既是奇函数也是偶函数
},所以f(x)=0,则f(x)既是奇函数也是偶函数
(2)去掉绝对值符号,根据定义判断.由
 得
得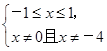 .
.故f(x)的定义域为[-1,0)∪(0,1],关于原点对称,且有x+2>0.
从而有f(x)=
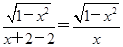 ,
,这时有f(-x)=
 =-f(x),故f(x)为奇函数.
=-f(x),故f(x)为奇函数.(3)因为f(x)定义域为[-1,1),所以f(x)既不是奇函数也不是偶函数.
(4)因为f(x)定义域为{-
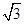 ,
,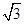 },所以f(x)=0,则f(x)既是奇函数也是偶函数
},所以f(x)=0,则f(x)既是奇函数也是偶函数
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
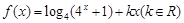 是偶函数.
是偶函数. 的值;
的值; ,若函数
,若函数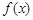 与
与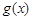 的图象有且只有一个公共点,求实数a的取值范围.
的图象有且只有一个公共点,求实数a的取值范围.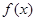 的定义域为
的定义域为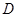 ,如果存在正实数
,如果存在正实数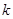 ,对于任意
,对于任意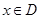 ,都有
,都有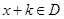 ,且
,且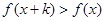 恒成立,则称函数
恒成立,则称函数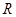 上的奇函数,且当
上的奇函数,且当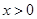 时,
时,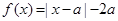 ,若
,若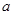 的取值范围是( )
的取值范围是( )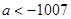

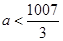
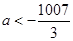
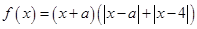 的图像是中心对称图形,则
的图像是中心对称图形,则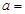 ( )
( )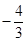
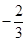
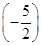 等于( )
等于( )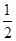
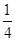
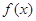 为奇函数,且当
为奇函数,且当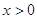 时,
时,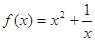 ,则
,则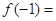 ( )
( )