Question

【题目】已知是定义在上的奇函数，当时，，当时，，若直线与函数的图象恰有7个不同的公共点，则实数的取值范围为_________.

Answer 1

【答案】（，）

【解析】

本题通过奇函数特征得到函数图象经过原点，且关于原点对称，利用得到函数类似周期性特征，从而可以画出函数的草图，再利用两个临界状态的研究，得到k的取值范围.

当时，，

．

当时，，

，

当，时，

，

，

函数是定义在R上的奇函数，

函数图象经过原点，且关于原点对称．

直线与函数的图象恰有7个不同的公共点，

当时，直线与函数的图象恰有3个不同的公共点，

由时的图象可知：

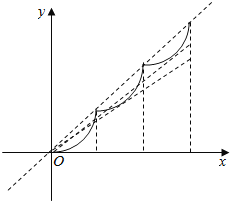
直线与函数的图象相切位置在时，直线与函数的图象恰有5个不同的公共点，

直线与函数的图象相切位置在时，直线与函数的图象恰有9个不同的公共点，

直线与函数的图象位置情况介于上述两种情况之间．

当时，

由得：

，

令，得：．

由得：

，

令，得：．

的取值范围为．

故答案为：．