题目内容
(12分)已知定义域为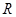 的单调函数
的单调函数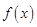 且
且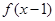 图关于点
图关于点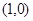 对称,当
对称,当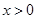 时,
时,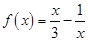 .
.
(1)求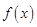 的解析式;
的解析式;
(2)若对任意的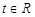 ,不等式
,不等式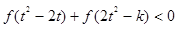 恒成立,求实数
恒成立,求实数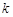 的取值范围.
的取值范围.
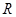 的单调函数
的单调函数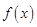 且
且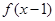 图关于点
图关于点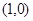 对称,当
对称,当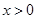 时,
时,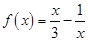 .
.(1)求
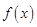 的解析式;
的解析式;(2)若对任意的
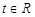 ,不等式
,不等式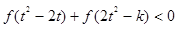 恒成立,求实数
恒成立,求实数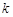 的取值范围.
的取值范围.(1) ;(2)
;(2) 。
。
 ;(2)
;(2) 。
。本试题主要是考查了函数的奇偶性以及函数的单调性的运用。
(1)定义域为 的函数
的函数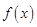 是奇函数
是奇函数  当
当 时,
时,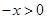
 又
又 函数
函数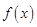 是奇函数
是奇函数

(2)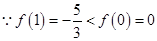 且
且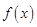 在
在 上单调
上单调  在
在 上单调递减,化简表达式得到求解。
上单调递减,化简表达式得到求解。
解:(1) 定义域为
定义域为 的函数
的函数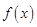 是奇函数
是奇函数  ----2分 当
----2分 当 时,
时,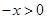
 又
又 函数
函数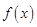 是奇函数
是奇函数
 -5分
-5分
综上所述 ----6分
----6分
(2)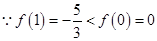 且
且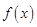 在
在 上单调
上单调  在
在 上单调递减 --8分由
上单调递减 --8分由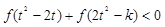 得
得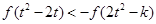
 是奇函数
是奇函数 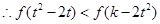 ,又
,又
 是减函数
是减函数 
 -----10分
-----10分
即 对任意
对任意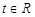 恒成立
恒成立 得
得 即为所求 -------12分
即为所求 -------12分
(1)定义域为
 的函数
的函数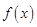 是奇函数
是奇函数  当
当 时,
时,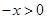
 又
又 函数
函数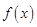 是奇函数
是奇函数

(2)
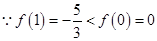 且
且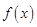 在
在 上单调
上单调  在
在 上单调递减,化简表达式得到求解。
上单调递减,化简表达式得到求解。解:(1)
 定义域为
定义域为 的函数
的函数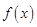 是奇函数
是奇函数  ----2分 当
----2分 当 时,
时,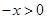
 又
又 函数
函数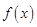 是奇函数
是奇函数
 -5分
-5分 综上所述
 ----6分
----6分(2)
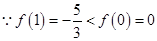 且
且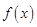 在
在 上单调
上单调  在
在 上单调递减 --8分由
上单调递减 --8分由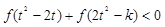 得
得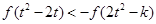
 是奇函数
是奇函数 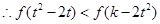 ,又
,又
 是减函数
是减函数 
 -----10分
-----10分即
 对任意
对任意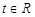 恒成立
恒成立 得
得 即为所求 -------12分
即为所求 -------12分
练习册系列答案
相关题目
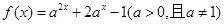
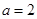 ,求
,求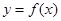 的值域
的值域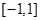 上有最大值14。求
上有最大值14。求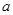 的值;
的值; 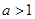 ,作出
,作出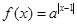 的草图,并通过图象求出函数
的草图,并通过图象求出函数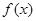 的单调区间
的单调区间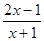 , x∈[3, 5]
, x∈[3, 5]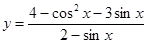 的最大值是( )
的最大值是( )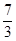
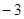
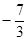
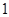
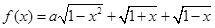 的最大值为
的最大值为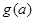 .
.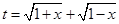 ,求
,求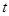 的取值范围;
的取值范围;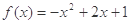
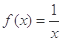
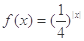
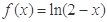
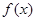 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,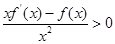 ,且
,且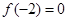 ,则不等式
,则不等式 的解集是( )
的解集是( )  ∪
∪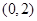
 ∪
∪
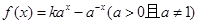 是定义域为R的奇函数.
是定义域为R的奇函数.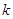 的值;
的值;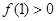 ,试判断函数单调性(不需证明)并求不等式
,试判断函数单调性(不需证明)并求不等式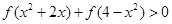 的解集;
的解集;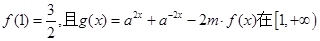 上的最小值为
上的最小值为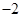 ,求
,求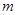 的值.
的值.