题目内容
(12分)已知函数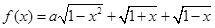 的最大值为
的最大值为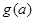 .
.
(1)设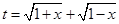 ,求
,求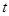 的取值范围;
的取值范围;
(2)求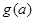 .
.
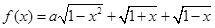 的最大值为
的最大值为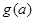 .
.(1)设
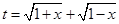 ,求
,求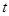 的取值范围;
的取值范围;(2)求
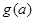 .
.(1) 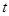 的取值范围
的取值范围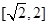 ; (2)
; (2) 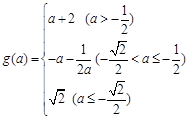
 的取值范围
的取值范围 ; (2)
; (2) 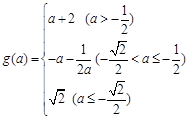
本试题主要是考查了二次函数的最值的运用。
(1)令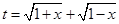 ,要使
,要使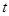 有意义,必须
有意义,必须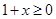 且
且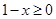
即 ∴
∴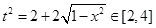 又∵
又∵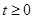
∴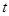 的取值范围
的取值范围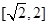
(2)由(1)知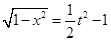
由题意知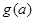 即为函数
即为函数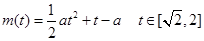 的最大值,那么需要对对称轴和定义域分类讨论得到结论。
的最大值,那么需要对对称轴和定义域分类讨论得到结论。
解:(1)令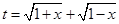 ,要使
,要使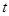 有意义,必须
有意义,必须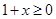 且
且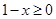
即 ∴
∴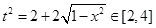 又∵
又∵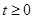
∴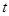 的取值范围
的取值范围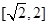
(2)由(1)知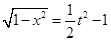
由题意知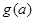 即为函数
即为函数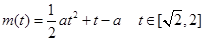 的最大值.
的最大值.
注意到直线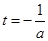 是函数
是函数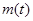 的对称轴,分以下几种情况讨论.
的对称轴,分以下几种情况讨论.
①当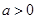 时,
时,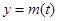 在
在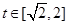 上单调递增.
上单调递增.
∴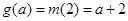
②当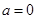 时
时 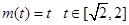 ∴
∴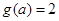
③当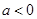 时 函数
时 函数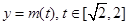 的图象开口向下的抛物线的一段.
的图象开口向下的抛物线的一段.
i)若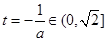 ,即
,即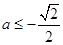 ,则
,则
ii)若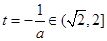 ,即
,即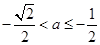 时,则
时,则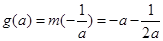
iii)若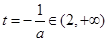 ,而
,而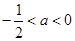 时,则
时,则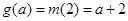
综上:有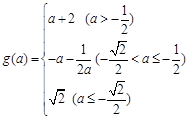
(1)令
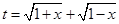 ,要使
,要使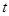 有意义,必须
有意义,必须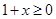 且
且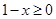
即
 ∴
∴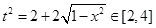 又∵
又∵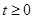
∴
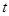 的取值范围
的取值范围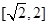
(2)由(1)知
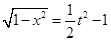
由题意知
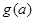 即为函数
即为函数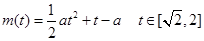 的最大值,那么需要对对称轴和定义域分类讨论得到结论。
的最大值,那么需要对对称轴和定义域分类讨论得到结论。解:(1)令
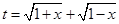 ,要使
,要使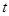 有意义,必须
有意义,必须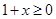 且
且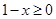
即
 ∴
∴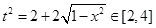 又∵
又∵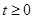
∴
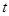 的取值范围
的取值范围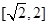
(2)由(1)知
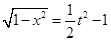
由题意知
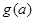 即为函数
即为函数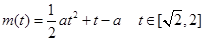 的最大值.
的最大值.注意到直线
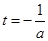 是函数
是函数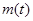 的对称轴,分以下几种情况讨论.
的对称轴,分以下几种情况讨论.①当
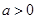 时,
时,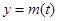 在
在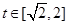 上单调递增.
上单调递增.∴
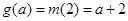
②当
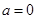 时
时 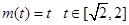 ∴
∴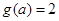
③当
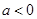 时 函数
时 函数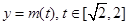 的图象开口向下的抛物线的一段.
的图象开口向下的抛物线的一段.i)若
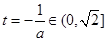 ,即
,即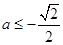 ,则
,则
ii)若
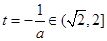 ,即
,即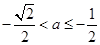 时,则
时,则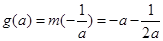
iii)若
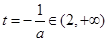 ,而
,而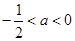 时,则
时,则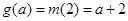
综上:有
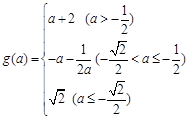

练习册系列答案
相关题目
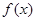 为定义在
为定义在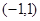 上的奇函数,当
上的奇函数,当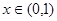 时,
时,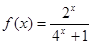 ;
;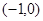 上的单调性,并给出证明.
上的单调性,并给出证明.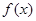 满足
满足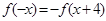 ,当
,当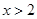 时,
时,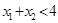 且
且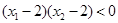 ,则
,则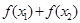 的值( )
的值( )  ,3],则函数F(x)=f(x)+
,3],则函数F(x)=f(x)+ 的值域是( )
的值域是( ) ]
]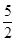 ,
,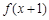 是偶函数,当
是偶函数,当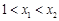 时,
时,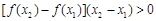 恒成立,设
恒成立,设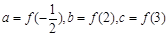 ,则
,则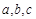 的大小关系为 ( )
的大小关系为 ( )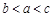

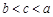
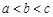
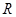 的单调函数
的单调函数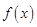 且
且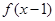 图关于点
图关于点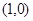 对称,当
对称,当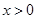 时,
时,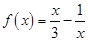 .
.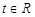 ,不等式
,不等式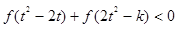 恒成立,求实数
恒成立,求实数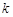 的取值范围.
的取值范围.
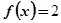 ,求x的值;
,求x的值;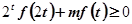 对于
对于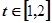 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数.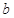 的值; (Ⅱ)判断函数
的值; (Ⅱ)判断函数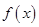 的单调性;
的单调性; ,不等式
,不等式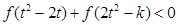 恒成立,求
恒成立,求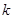 的取值范围.
的取值范围. 满足:
满足: ,且对于任意的
,且对于任意的 ,都有
,都有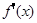 <
< ,则不等式
,则不等式 >
> 的解集为 。
的解集为 。