题目内容
(12分)已知函数f(x)=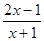 , x∈[3, 5]
, x∈[3, 5]
(1)判断f(x)单调性并证明;(2)求f(x)最大值,最小值.
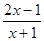 , x∈[3, 5]
, x∈[3, 5](1)判断f(x)单调性并证明;(2)求f(x)最大值,最小值.
(1)f(x)在[3,5]上↑;(2)ymax=f(5)=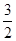 ymin=f(3)=
ymin=f(3)=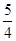
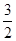 ymin=f(3)=
ymin=f(3)=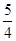
本试题主要是考查了函数的单调性和函数的 最值问题的运用
(1)先分析函数的单调性结合定义得到证明。
(2)根据第一问的结论,分析得到最值。
(1)f(x)= ↑
↑
任取3≤x1<x2≤5
则f(x1)-f(x2)=2-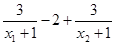 =
=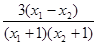 <0
<0
即f(x1)<f(x2) ∴f(x)在[3,5]上↑
(2)由(1)知ymax=f(5)=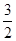 ymin=f(3)=
ymin=f(3)=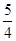
(1)先分析函数的单调性结合定义得到证明。
(2)根据第一问的结论,分析得到最值。
(1)f(x)=
 ↑
↑任取3≤x1<x2≤5
则f(x1)-f(x2)=2-
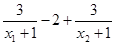 =
=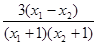 <0
<0即f(x1)<f(x2) ∴f(x)在[3,5]上↑
(2)由(1)知ymax=f(5)=
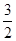 ymin=f(3)=
ymin=f(3)=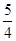

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
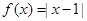
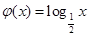 与函数
与函数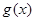 的图象关于
的图象关于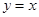 对称,
对称,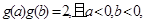 则
则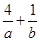 的最大值为 ;
的最大值为 ; 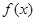 是定义在
是定义在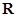 上的偶函数,对任意的
上的偶函数,对任意的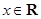 ,都有
,都有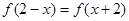 ,且当
,且当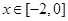 时,
时,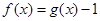 ,若关于
,若关于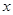 的方程
的方程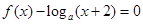
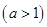 在区间
在区间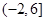 内恰有三个不同实根,则实数
内恰有三个不同实根,则实数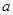 的取值范围是 。
的取值范围是 。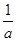 -
-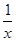 (a>0,x>0).
(a>0,x>0).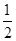 ,2]上的值域是[
,2]上的值域是[ 的图像关于原点对称,并且当
的图像关于原点对称,并且当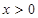 时,
时,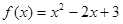 ,试求
,试求 上的表达式,并画出它的图像,根据图像写出它的单调区间。
上的表达式,并画出它的图像,根据图像写出它的单调区间。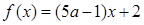 在
在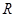 上是增函数,则
上是增函数,则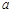 的取值范围是( )
的取值范围是( )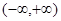
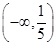
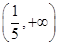
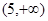
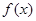 满足
满足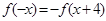 ,当
,当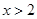 时,
时,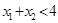 且
且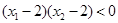 ,则
,则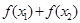 的值( )
的值( )  ,3],则函数F(x)=f(x)+
,3],则函数F(x)=f(x)+ 的值域是( )
的值域是( ) ]
]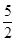 ,
,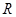 的单调函数
的单调函数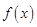 且
且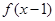 图关于点
图关于点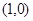 对称,当
对称,当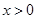 时,
时,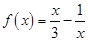 .
.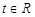 ,不等式
,不等式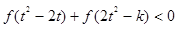 恒成立,求实数
恒成立,求实数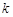 的取值范围.
的取值范围.