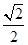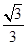题目内容
已知椭圆的焦点为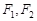 ,P是椭圆上一动点,如果延长F1P到Q,使
,P是椭圆上一动点,如果延长F1P到Q,使 ,那么动点Q的轨迹是( )
,那么动点Q的轨迹是( )
| A.椭圆 | B.双曲线 | C.抛物线 | D.圆 |
D
解析试题分析:充分利用平面几何图形的条件特点,结合椭圆的定义,得到|F1Q|为定长,从而确定动点Q的轨迹是个什么图形解析:∵|PF1|+|PF2|=2a,|PQ|=|PF2|,∴|PF1|+|PF2|=|PF1|+|PQ|=2a,即|F1Q|=2a,∴动点Q到定点F1的距离等于定长2a,故动点Q的轨迹是圆.故答案D
考点:求轨迹方程
点评:本题考查了求轨迹方程的方法及定义法.定义法:若动点轨迹的条件符合某一基本轨迹的定义(如椭圆、双曲线、抛物线、圆等),可用定义直接探求

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
抛物线 的焦点F是椭圆
的焦点F是椭圆 的一个焦点,且它们的交点M到F的距离为
的一个焦点,且它们的交点M到F的距离为 ,则椭圆的离心率为
,则椭圆的离心率为
A. | B. | C. | D. |
如图, 是平面
是平面 的斜线段,
的斜线段, 为斜足。若点
为斜足。若点 在平面
在平面 内运动,使得
内运动,使得 的面积为定值,则动点
的面积为定值,则动点 的轨迹是( )
的轨迹是( )
| A.圆 | B.椭圆 |
| C.一条直线 | D.两条平行直线 |
设 、
、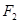 分别是椭圆
分别是椭圆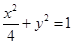 的左、右焦点,
的左、右焦点, 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且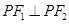 ,则点
,则点 的横坐标为
的横坐标为
A.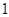 | B.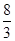 | C.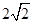 | D.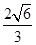 |
已知抛物线Cl:y2= 2x的焦点为F1,抛物线C2:y=2x2的焦点为F2,则过F1且与F1F2垂直的直线 的一般方程式为
的一般方程式为
| A.2x- y-l=0 | B.2x+ y-1=0 |
| C.4x-y-2 =0 | D.4x-3y-2 =0 |
曲线 +
+ =1.(m<6) 与
=1.(m<6) 与 +
+ =1.(5<m<9)的( )
=1.(5<m<9)的( )
| A.准线相同 | B.离心率相同 | C.焦点相同 | D.焦距相同 |
 的双曲线与圆
的双曲线与圆 的一个交点,则
的一个交点,则 = ( )
= ( )



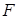 是抛物线
是抛物线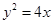 的焦点,准线与
的焦点,准线与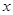 轴的交点为
轴的交点为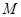 ,点
,点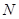 在抛物线上,且
在抛物线上,且 ,则
,则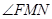 等于( )
等于( )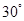
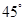
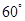
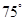
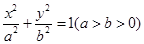 与双曲线
与双曲线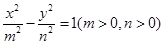 有相同的焦点
有相同的焦点 和
和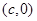 ,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为
,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为